Challenges and limitations of quantifying brain connectivity in vivo with diffusion MRI

Cardiff University Brain Research Imaging Centre, School of Psychology, Cardiff University, Park Place, Cardiff, UK

Corresponding Author:

Derek K Jones
Cardiff University Brain Research Imaging Centre
School of Psychology, Cardiff University, Park Place, Cardiff, UK
Tel: +44 292 087 9412
Fax: +44 292 087 0339 E-mail: jonesd27@cf.ac.uk

Abstract

This article addresses whether or not diffusion MRI, a noninvasive technique that probes the microstructural aspects of tissue, can be used to quantify the white matter connectivity of the human brain in vivo. It begins by studying the motivation, that is, the increasing trend to look at ‘functional connectivity’ in the brain, which implies that the brain operates as a distributed network of active locations. A brief summary of diffusion MRI and fiber tracking is given and the early applications of diffusion MRI to study connectivity are reviewed. A close and critical inspection is then made of the limitations inherent in these different approaches, challenging the notion that it is possible to quantify brain connectivity in vivo with diffusion MRI. Finally, steps toward improving quantification of connectivity, by integrating information from other techniques, are suggested.

Keywords

connectivity ▪ diffusion ▪ fractional anisotropy ▪ MRI ▪ probabilistic ▪ tractography ▪ white matter

The aim of this article is to provide a critical overview of the current uses of diffusion MRI to quantify white matter connectivity. There are two main focuses of this work. The first is on quantification and the second on interpretation. Some cynics might say the technique is often abused. Others would say that results are frequently misinterpreted owing to the techniques being used before they were ready for general use or fully understood. The aim of this article, therefore, is to provide an honest and frank overview – bringing the shortcomings of the use of diffusion MRI out in the open – so that the reader can appreciate potential pitfalls and shortcomings.

Many, if not all, of the issues raised in this article are known and appreciated by those who are developing diffusion MRI methods, and the intention is not to teach such researchers their own business; rather, the aim of this article is to summarize the limitations and collate, into one reference article, collective wisdom and common sense relating to the use of diffusion MRI to probe connectivity. In this sense, this article presents a set of challenges to be overcome and will hopefully inspire researchers to work on these issues and develop strategies for remediation. It will hopefully act as useful guidance for those who are about to start, or have already started, using off-the-shelf software packages without having considering some of the limitations of such packages.

Background

Functional networks

It is increasingly recognized that to fully understand the function of the brain the ‘localizationist’ approach of yesteryear is no longer valid; rather, the brain must be considered as a distributed network of activity, with information exchanging constantly between different cortical and subcortical regions. Until recently, the focus of noninvasive neuroimaging research (and most invasive recording methods) had been on looking at brain ‘activity’, that is, increases in electrical activity (or their accompanying hemodynamic concomitants) within cortical and subcortical gray matter structures, using a range of techniques that include, but are not limited to, functional MRI, near-infra-red spectroscopy, electroencephalography, magnetoencephalography and invasive electrode recordings. Originally focused on determining which parts of cortex are ‘active’ during a task (compared with a resting or control period), analysis methods have now developed to look for synchronicity, temporal correlation or phase coupling of changes in signals in different parts of the brain. The rationale is that if temporal variations in the signals recorded at two or more locations are correlated then there must be some form of exchange of information between those regions – leading to the concept of ‘functional connectivity’ [1]. This form of analysis can be extended in several ways: by observing naturally occurring oscillations in brain activity in the brain ‘at rest’ (with the explicit assumption that the brain is not performing any particular task), coupling of signals between the same cortical regions has been reproducibly identified, which has led to the idea of ‘resting state connectivity’ [2,3]. Furthermore, the influence of input into a functional network can be modeled and used to predict the influence that activity in one cortical region has over activity in another in an approach that is labeled ‘effective’ connectivity [4]. These are just some examples of improved attempts to characterize the functional networks of the brain using noninvasive methods.

White matter

However, with very few exceptions, such analyses have not concerned themselves with the mechanism by which the information, which causes signals in different regions of the brain to be coupled, actually passes between those two regions (either via a direct or indirect pathway taking in other regions en route) and, put bluntly, seem to have a total disregard for anatomy. However, a glance at a standard structural MRI scan of the brain reveals that much of the brain (approximately 45%) comprises white matter, the predominantly myelinated axon bundles that originate in the neurons and carry electrical impulses between adjacent gyri and between different lobes of the brain. Thus, to fully understand the characteristics of a brain network and, therefore, to understand the operation of the brain as a whole (or even a subcomponent of it), the physical connections that mediate information transfer between different cortical regions must be characterized. A statement that serves perfectly as a motto for motivating the study of white matter connectivity comes from Marsel Mesulam, “nothing defines the function of a neuron better than its connections” [5]. (Thanks to Marco Catani, Institute of Psychiatry, London, UK for first alerting me to this phrasing.) However, until relatively recently, as highlighted by Crick and Jones’s commentary on the “backwardness of human neuroanatomy” [6], there were no methods available for looking at the white matter anatomy that could be safely used in vivo.

Diffusion MRI

Although insights into white mater anatomy can be garnered from painstaking and timeconsuming invasive tracer methods, they are not extendable to the study of whole brains and clearly cannot be used in a research setting, prompting Crick and Jones’s commentary [6]. One technique that addresses this issue and has generated great optimism (and impressive results) is diffusion MRI. There are numerous reviews on the principles of diffusion MRI [7–11], and now several texts [12–14], so a detailed review and introductory references will not be given here. However, a sufficient summary of the principles is provided for readers new to the field.

Modifications to an MRI pulse sequence can enhance the sensitivity of the MRI signal to the microscopic (on the scale of 10 μm) motion of water molecules that is caused by thermally driven random motion (diffusion) such that the MRI signal becomes increasingly attenuated as the mean displacement of water molecules within the image voxel increases. The effect of tissue microstructure (e.g., cell membranes and macromolecules) serves to hinder the movement of water molecules, which, in turn, modulates the diffusion-weighted signal intensity. In tissue that appears randomly organized on the scale of the voxel (typically with dimensions of 1.5–2.5 mm), the reduction in the magnetic resonance signal caused by diffusion will be independent of the direction in which it is measured. However, in ordered tissue, such as axonal bundles, the motion of water molecules is less hindered along the bundle than in the perpendicular direction; leading to an orientational dependence of the signal loss. Different approaches to modeling the cause of this signal loss have been adopted in the literature, with the most popular being that the diffusion process can be modeled as having multimodal Gaussian behavior, and characterized by a single tensor model. From the tensor, several indices can be derived, including the orientationally averaged diffusivity and the fractional anisotropy (which characterizes the extent to which the apparent diffusion coefficient varies according to orientation). Furthermore, the tensor framework provides an estimation of the direction in which the diffusivity of the fitted tensor is greatest (i.e., the principal eigenvector). Such orientational information can be exploited to produce voxel-wise maps of fiber orientation or integrated to form continuous trajectories in a family of techniques collectively referred to as tractography. Tractography algorithms typically fall into two categories: deterministic (where, at each point in space, there is only one estimate of fiber orientation – usually based on the principal eigenvector – and a pathway is reconstructed by moving from point-to-point by following the principal eigenvector) and probabilistic (where, at each point in space, there is a distribution of possible fiber orientations – and pathways are propagated repeatedly through this field, each time drawing a random sample from the distribution of orientations – leading to a distribution of possible pathways between two points). Refinements in the analysis of diffusion MRI data have largely been in modeling the source of the signal variation in the presence of complex tissue architecture (e.g., fibers kissing, crossing, splaying, twisting and fanning), leading to techniques, such as diffusion spectrum imaging [15], q-ball imaging [16], spherical harmonic deconvolution [17], persistent angular structure MRI [18], models of diffusion, such as composite hindered and restricted model of diffusion (CHARMED) [19], and in the development of probabilistic algorithms.

In light of the dearth of previously available techniques for assessing white matter, and in a climate in which there is increasing focus on the brain as a connected network, it is easy to appreciate why diffusion MRI-based techniques have become rapidly adopted by the neuroscience and clinical research communities as a tool for probing/ assessing white matter connectivity. How far can these methods be relied on and what are the limitations on using diffusion MRI to assess tissue connectivity?

What do we mean by ‘connectivity’?

One perennial problem that remains to be resolved is what is actually meant by ‘connectivity’ in this context. Whether or not connectivity can be measured could be perceived as a question of semantics. However, if referring to quantification of connectivity, as we are in this article, then a numerical scale on which connectivity can be assessed must be referred to. What numbers are appropriate? The number of axonal projections between two regions would seem to be one good measure; the more axonal connections between two regions, the more ‘connected’ they might be considered to be. This is viewing the concept from a purely structural aspect. However, the efficiency of, or capacity for, information transfer between two regions might also be considered. Relating back to earlier comments regarding functional connectivity, if two regions can communicate efficiently they may be deemed to be more ‘strongly connected’. In this case, the microstructural attributes of the tissue must be considered. The speed with which information can be propagated along a myelinated axon is related to its diameter, the density of axons, the internodal spacing of the myelin and the degree of myelination itself. Indices that provide quantitative insights into some of these metrics for whole brain are coming online [19–23], but are not yet routinely incorporated into assessment of brain connectivity. I would argue that the purpose of studying white matter ‘connectivity’ (maintaining this concept as an abstract form for the moment) is, ultimately, to understand the function of brain. Consequently, variation in whatever metrics are used to derive with must have concomitant variation in brain function – otherwise the metric is uninteresting and not useful. (The counter-argument that a metric that quantifies an aspect of white matter properties that can vary with absolutely no impact on brain functionality is still an interesting metric seems entirely illogical.) This caveat, therefore, for whether we can derive a useful index from diffusion MRI to quantify ‘connectivity’ is to be borne in mind in what follows.

Diffusion as a tool for quantifying brain connectivity

So can diffusion MRI be used to quantify brain connectivity? Certainly a survey of article titles in the literature (PubMed search terms: diffusion [title/abstract] and MRI [title/abstract] and connectivity [title]) would suggest that many people seem to have thought so at one point or another. In fact, the author of this article counts himself amongst these people, having written the first paper to satisfy these search terms [24]. (People in glass houses should not throw stones.) Looking through the early literature (1998 onwards), it appears that studies reporting to probe connectivity with diffusion MRI have fallen into two categories, those based on localized voxel-based metrics and those based on tractographic-based reconstructions of longer-range connectivity.

However, before discussing diffusion MRI, it is interesting to note that many previous studies have carried out voxel-based morphometric or simple region-of-interest-based studies of structural (i.e., T1-weighted) magnetic resonance data that have revealed group differences in white matter volume or hyperintensity in different disease conditions. However, while such studies have discussed changes in white matter, in my opinion, these studies never posited the notion that connectivity was being probed. However, the authors of these studies were performing voxel-based assessments of the very stuff that mediates brain connectivity (i.e., white matter).

Voxel-based assessment of brain connectivity?

The first suggestion that diffusion MRI might be used to probe white matter connectivity was made by Monte Buchsbaum, in which he looked for reductions in white matter anisotropy in schizophrenics compared with controls and compared such MRI results with those obtained from ¹⁸F-fluorodeoxyglucose PET [25]. This was achieved by taking a voxel-based morphometric approach (i.e., spatially aligning each individual dataset to a common reference space) and, on the assumption that each voxel in the aligned dataset corresponds to the same anatomical structure, performing a voxel-by-voxel group-wise comparison of anisotropy data (an approach that has since been adopted by many groups to study diffusion MRI data in a range of disease conditions).

Observing localized alterations in fractional anisotropy in the white matter passing between the putamen and frontal lobe, Buchsbaum and colleagues interpreted this finding as a ‘connectivity deficit’ and stated that “the diffusion tensor method obtains structural connectivity information based on physical features of the white matter” [25]. Therefore, as early as 1998, the link between voxel-based diffusion MRI measures and connectivity was made. The naming of this as ‘connectivity’ was presumably motivated by: the recently (at the time) proposed theory that schizophrenia represents a ‘disconnection’ syndrome [26] (based on the inference from functional data that there is a disruption of prefronto–temporal interactions in schizophrenia) and an acknowledgement to the fact that white matter mediates connectivity.

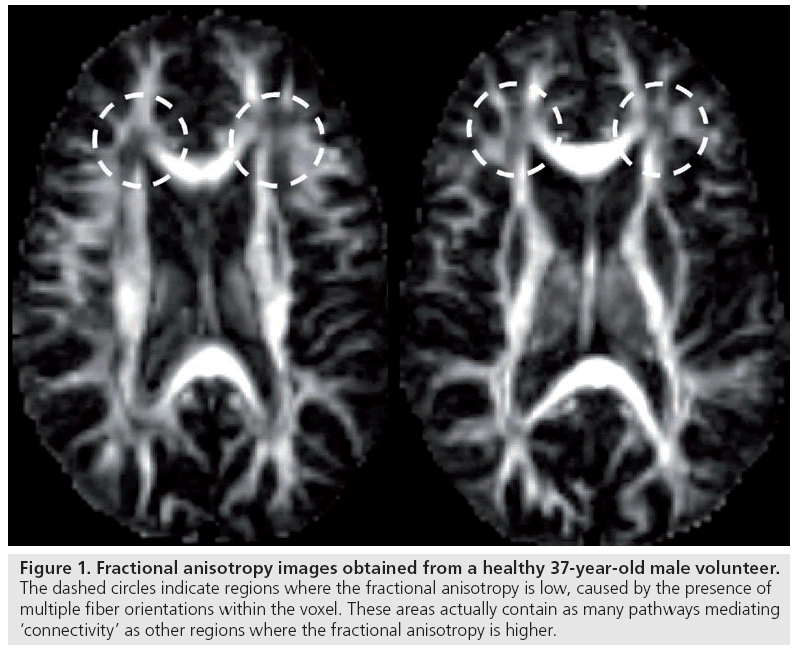
Can these voxel-based measures of tissue anisotropy, where each voxel location is treated in isolation from its neighbors, really be considered to be quantifying connectivity? It is important to remember the nature of the signal that is being compared. The anisotropy metric is simply a measure of the extent to which the mean square displacement of water molecules within a volume of tissue (typically to the order of 2.5 × 2.5 × 2.5 mm³) depends on the direction in which it is measured. As such, there are several factors that can modulate the diffusion anisotropy metric [27], including, but not limited to, the axon diameter distribution, the axon density, the myelination of the fibers and, as demonstrated by Pierpaoli et al., the architectural paradigm of the white matter fibers (in other words, how are the individual axons orientated with respect to each other within the voxel) [28]. As such, the anisotropy is not a very specific measure at all. Newcomers to the field of diffusion MRI may be surprised by the fact that regions with the lowest anisotropy within deep white matter can often contain the largest number of axons passing through them; however, owing to their incoherent orientations, diffusion displacements are no longer preferentially hindered along a single axis and the anisotropy of the voxel-averaged displacements is low (Figure 1).

Figure 1: Fractional anisotropy images obtained from a healthy 37-year-old male volunteer. The dashed circles indicate regions where the fractional anisotropy is low, caused by the presence of multiple fiber orientations within the voxel. These areas actually contain as many pathways mediating ‘connectivity’ as other regions where the fractional anisotropy is higher.

Such a reduction in the voxel-averaged anisotropy, where there may, in fact, be more pathways mediating connections, can lead to apparently paradoxical observations. For example, ‘elevation’ of anisotropy can be observed in disease if there is selective destruction of one particular fiber orientation. Furthermore, Tuch et al. reported an initially very surprising result in which they attempted to correlate reaction time on a four-choice reaction time test with white matter fractional anisotropy (FA) [29]. Tuch et al. found a linear correlation between reaction time and FA, but this was a positive correlation (i.e., the higher the anisotropy, the longer the reaction time). This certainly goes against the idea that voxel-wise measurements of FA alone can provide a useful measure of efficiency of information transfer. However, this anomaly can be explained by the fiber architecture in the vicinity of the region that Tuch et al. found the significant correlation. In this region, there are two main fiber populations that merge at different orientations – those that come from the corpus callosum (potentially less interesting) and those that form part of the visual system. If the anisotropy and/or the volume component of the visual system fibers is increased, potentially improving efficiency of information transfer throughout the visual system, then the net result is a reduction in anisotropy in the vicinity of the interface of the callosal and visual fibers – much as in the regions of low FA in Figure 1. This serves as a very strong argument against the use of voxel-wise measurements of FA to make inferences on connectivity and capacity for information transfer.

Consider an alternative notion of ‘connectivity’, posited earlier, namely that this might reflect the number of axonal connections, then this further highlights inadequacy of voxel-based FA measurements. First, in a thought experiment, imagine that the myelination of a white matter bundle is selectively reduced, but all other attributes of the white matter are kept the same (axon density, diameter distribution and alignment, and membrane permeability), the anisotropy would definitely change but, based on the argument that ‘connectivity’ is the number of axonal connections to that region, the ‘connectivity’ would not change. Similar arguments can be applied to other changing attributes, such as the axon diameter distribution and membrane permeability, all of which would affect measures of diffusion anisotropy, but none of which would change the ‘number of axons’ in the region. Thus, we seem to be onto a loser. Diffusion MRI does not and cannot currently be used to identify the number of axons in a voxel. Therefore, based on these assumptions, although telling us something nonspecific about the existence of differences in white matter microstructure, voxel-based measurements of diffusion attributes in isolation do not allow the quantification of connectivity per se, and it is perhaps time to temper descriptions of results to avoid claiming that ‘connectivity’ is reduced on the basis of such measurements.

Tractographic assessment of brain connectivity Deterministic approaches

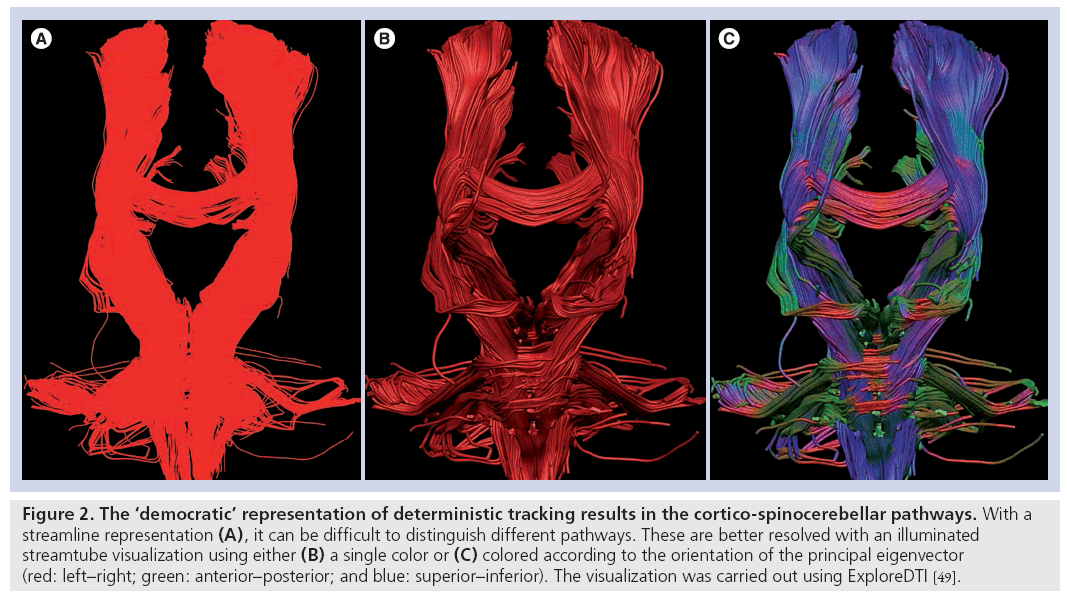
Shortly after the appearances of the first studies that made inferences on brain connectivity based on localized (voxel-by-voxel) diffusion measurements, attempts to map white matter pathways based on diffusion MRI appeared in the literature [24,30–32]. The initial fiber-tracking algorithms followed similar strategies by considering one estimate of fiber orientation (the principal eigenvector of the diffusion tensor) at the center of each imaging voxel and using this information to determine whether different points of the brain could be reached by following this orientational information. In such algorithms, only one estimation of fiber orientation is used at each point in space, so the tracking result is always the same when the tracking algorithm is run on the same data; hence, these approaches are called ‘deterministic’. The most popular deterministic algorithm is to follow ‘streamlines’ through the eigenvector field. This approach has produced very useful insights into ‘what is connected to what’. However, the output of these algorithms is always the same (i.e., whether or not there is a pathway through the data between two points in space). As such, the answer has a binary form: 0 = no pathway; and 1 = pathway. No more inferences can be drawn from the data, and certainly nothing more quantitative can be said about connectivity within an individual’s dataset. In other words, ‘connections’ but not ‘connectivity’ are being studied. Furthermore, there is absolutely no indication of the confidence that we can assign to a particular tracking result and, thus, all tracts are usually represented with a uniform color mapping (or perhaps encoding by the principal eigenvector orientation) (see Figure 2).

Figure 2: The ‘democratic’ representation of deterministic tracking results in the cortico-spinocerebellar pathways. With a streamline representation (A), it can be difficult to distinguish different pathways. These are better resolved with an illuminated streamtube visualization using either (B) a single color or (C) colored according to the orientation of the principal eigenvector (red: left–right; green: anterior–posterior; and blue: superior–inferior). The visualization was carried out using ExploreDTI [49].

In other words, an erroneous and completely artifactual pathway that has no correspondence with the underlying neuroanatomy, is as democratically represented as a reconstructed pathway through the data, which conforms exactly to the course of a major white matter pathway.

The adoption of enhanced visualization strategies, such as illuminated stream tubes [33], that give the tract reconstructions a palpable quality simply add to the impression that what the viewer is looking at is ‘real’ in some sense and, thus, a naive viewer will regard all reconstructed pathways as equally trustworthy. However, errors in the reconstructed pathways, hidden by such visualizations, can lead to serious problems – especially when relied upon in neurosurgical interventions – as reported by Kinoshita et al. [34].

Probabilistic approaches

The main limitation of the streamline deterministic tracking approach with diffusion tensor MRI data is that it does not account for either systematic errors or stochastic errors in the prediction of fiber orientation. Regarding systematic errors, it is now widely accepted that in regions of complex fiber architecture (i.e., any architectural paradigm that deviates from a uniform fiber orientation, including crossing, twisting, splaying, bending and kissing fibers), the tensor model (and, therefore, the principal eigenvector) is inadequate for capturing the different fiber orientations. There have been a multitude of approaches for improved resolution of such complex architectures [15–19].

In relation to stochastic errors in fiber orientation, regardless of whether a simple tensor model or a more advanced high angular resolution diffusion images-style analysis is used, it must be remembered that diffusion MRI is an inherently noisy technique. As such, the noise in the individual diffusion-weighted images will propagate through the modeling/analysis pipeline to produce uncertainty in estimates of fiber orientation [35]. Thus, when the same individual is scanned and rescanned in exactly the same location and a deterministic tracking algorithm on the two datasets is employed, it is easy to see why the results would differ, as the reconstructed streamline is a summation of noisy estimates of fiber orientation and each tracking analysis would have used a different estimate. Importantly, uncertainty in fiber orientation is not uniformly distributed throughout the brain [35] and, thus, the variability that one obtains with a tracking result will be dependent on where in the brain the tracking occurs.

The majority of tractography algorithms still use a streamline evolution for each individual pathway, following a smooth trajectory through the estimates of fiber orientation. However, the key difference is that, at each point in space, there is now a distribution of estimates of fiber orientation from which to choose the next propagation direction. Thus, in contrast to deterministic tracking algorithms, probabilistic tracking algorithms generate multiple pathways from a given point in space. The end result is a set of multiple pathways (streamlines) passing through the seedpoint. The information contained within this set of streamlines is then conventionally summarized by counting how many times each voxel in the volume of interest (usually the whole brain) is intersected by a streamline, and is usually expressed as a percentage (i.e., number of streamlines passing through the voxel divided by the number of streamlines passing through the initial seedpoint). The first studies of probabilistic fiber tracking was published by Martin Koch and colleagues [36,37]. Interestingly, these works use the phrase ‘anatomical connectivity’ in their titles and they produced a map with varying degrees of ‘connectivity’ between them. This algorithm worked on a Monte Carlo random walk between voxels, with the frequency of jumping in a particular direction being dictated by the projected apparent diffusion coefficient profile in each voxel. A later implementation of probabilistic tractography assumed a heuristic model relating the anisotropy of the tensor to the uncertainty in fiber orientation to produce a ‘probabilistic index of connectivity’ [38]. Since these early papers, there has been a vast array of papers on probabilistic tracking. Many of these differ only in the way in which the uncertainty in fiber orientation is derived and include (in a nonexhaustive list) heuristic models [38], resampling bootstrapping [39], residual bootstrapping [40] and Bayesian methods [41]. Once the uncertainty is derived, the streamlining algorithm is run repeatedly to build up a pattern of possible paths through the data.

Interpretation

Connection strength or just a tangent to the space curve? Connection strength

Perhaps owing to the aforementioned focus on studying the brain as a network, researchers in the field have been predisposed to focus on connectivity. As previously discussed, deterministic tracking only gives a binary answer about whether something is connected to something else. With probabilistic tracking, the index varies between zero (none of the seeded streamlines reached the other voxel) to one (all of the seeded streamlines reached the other voxel). Perhaps more than in any other area of diffusion MRI, there have been quantum leaps in the interpretation of this form of quantitative data.

At base level, the most conservative interpretation of this kind of information is that it simply allows confidence to be assigned to the existence of a pathway through the data between two points [39]. In other words, one can infer how likely is it that such a pathway through the data could have arisen by chance alone. More plainly, it demonstrates how reproducible the pathway through the data is. At this stage, it is important to make a clear distinction between precision (the reproducibility of the result) and the accuracy (the difference between the measured and true data). Probabilistic tracking results give an indication of the precision of the tracking result but say nothing about accuracy. However, when viewing a probabilistic tract map, it is incredibly difficult for the observer not to assume that these maps provide the most likely position of the underlying white matter pathway and, therefore, in voxels with high values, to be more confident of accurate localization of the underlying pathway. This is a mistake often made by those inexperienced in the field. To appreciate this, Figure 3 shows a probabilistic tracking result obtained from a seedpoint placed in the left corticospinal tract in which there is a continuous band of highest voxel values in the map that crosses the pons and continues to ascend the contralateral corticospinal tract. The eye naturally follows this pattern and, without additional guidance, an observer would assume that this represents a continuous connected pathway. Although this represents the most precise (reproducible) pathway, it is also completely inaccurate with regard to the presence of a true anatomical ‘connection path’ along this route. Any glance at a basic neuroanatomy book will reveal that this is a completely artifactual connection. To reiterate, probabilistic tracking algorithms produce maps of precision and may be highly inaccurate. They are as equally susceptible to systematic errors in the data acquisition and analysis pipeline as deterministic algorithms.

Figure 3: Example of a probabilistic tracking result for the selected seedpoint placed in the corticospinal pathway. (A) Shows the individual streamline trajectories reconstructed from the seedpoint (location highlighted by the arrow in (A) and cross-hairs in the (B)) as part of the algorithm, while (B) shows the same data mapped by determining how many seedpoints intersect a particular voxel. ‘Hotter’ colors represent more streamlines and ‘cooler’ colors fewer. In this example, the most reproducible pathway is to follow a trajectory inferiorly from the seedpoint, across the pons and then ascend the contralateral corticospinal pathway. This result, although the most reproducible, is anatomically incorrect.
Adapted with permission from [41].

The results in Figure 3 were obtained within a normal healthy brain, but the reader will readily realize that the effect of pathology in disease can confound matters further. In areas of complex fiber architecture, where the diffusion behavior is not adequately characterized by a single prolate (cigar-shaped) tensor, the streamlines in probabilistic tracking algorithms will naturally spread in such locations, following the different possible pathways. For example, if the pathology is such that it selectively disrupts all but one pathway, a single pathway that is well described by a prolate tensor has high anisotropy and presents the only option for the streamlines in the tracking algorithm to follow is left. Consequently, the number of streamlines propagated along this remaining pathway is going to be much higher than when the other options were available. Thus, without due care and attention, this could be interpreted as an increase in connectivity along this remaining pathway. To see an example of this in action, where the integrity of one pathway is compromised by Wallerian degeneration, leading to ‘increased connectivity’ in another, the reader is referred to [42].

In some cases, probabilistic tracking appears to do a good job and the continuous band of highly visited voxels does correspond well to known anatomy. Typically, this is judged by looking at well-known white matter structures (i.e., in the large white matter fasciculi where the anisotropy is high, there may be fewer crossing fibers and the uncertainty in fiber orientation is lower). In such pathways, there is less room for variance in the estimation of fiber orientation and, therefore, accumulated errors in the tract reconstruction – thus, the most precise path will often be accurate.

Such maps are sometimes referred to as ‘likelihood’ maps, which are interpreted as showing the likelihood that the path of continuous voxels reflects the existence of a true anatomical (white matter) pathway. Again, based on Figure 3 we can see the limitations of such an assumption. More frequently, the interpretation/labeling of such maps is ‘connection probability’, which has led to people blurring the boundary between probability of a connection in the data and probability of a white matter pathway forming that connection. From the foregoing discussion, one can already see that this may be a step too far in interpretation.

Finally, the least conservative interpretation, but certainly the most attractive, is that these maps provide an index of ‘connectivity’ and the absolute number indicates ‘connection strength’, with authors taking license to talk about ‘region A being more strongly connected to region B’.

Tangent to the space curve

While such interpretations are indeed attractive and widespread, are they justified and can they be used in the aforementioned concept of connectivity? That is, either a physical attribute reflecting the number of axonal connections between two points or the capacity to carry impulses/ information between two points? The answer is clearly no. The only information that goes into the calculation of these maps is an estimate of the tangent to the space curve [32] (e.g., either from an eigenvector from diffusion tensor imaging, or a peak in some other reconstruction from high angular resolution diffusion image style analyses [15–19]) and, in the case of probabilistic tractography, the associated uncertainty. A true test of a robust measure of ‘connection strength’ or ‘connectivity’ is that it should not be dependent on the parameters set on the MRI scanner during acquisition. However, the uncertainty in fiber orientation will be affected by the signal-to-noise ratio in the data and the total number of measurements used to estimate the fiber orientation. The lower the signal-to-noise ratio and/or the lower the number of measurements taken, the noisier the estimate of fiber orientation will be and, thus, the lower the ‘connection probability’ between different points will be. By contrast, capturing a real, physical attribute of the tissue would not be sensitive to such variations in data quality/acquisition.

Favoring the shortest, straightest and simplest path

If the space curve (fiber trajectory) is straight, then the tangent is a good approximation to the curve at all points along the path. By contrast, if the path is curved, then the tangent is only indicative of/parallel to the trajectory of the streamline at the infinitesimal point at which the tangent is estimated. At any distance away from this point the estimate of the tangent to the space curve becomes less accurate. Furthermore, the more curved the path, the more rapidly the error in the path will increase with distance from that estimate. Thus, the accuracy and precision with which a curved path can be followed is lower than that for a straight path. Even for a perfectly straight path, owing to the uncertainty in each estimate of the tangent, there will be accumulated error and, therefore, the longer the path, the harder it will be to precisely and accurately reconstruct. Thus, the length and shape of the tract alone influences tracking accuracy and precision and, therefore, will also influence any index of ‘connectivity’ derived from probabilistic tractography. Furthermore, if a fiber system branches ‘downstream’ of the initial seedpoint, the total number of reconstructed streamlines will be divided (evenly or unevenly) along the two branches, thereby reducing the ‘index of connectivity’ yet again.

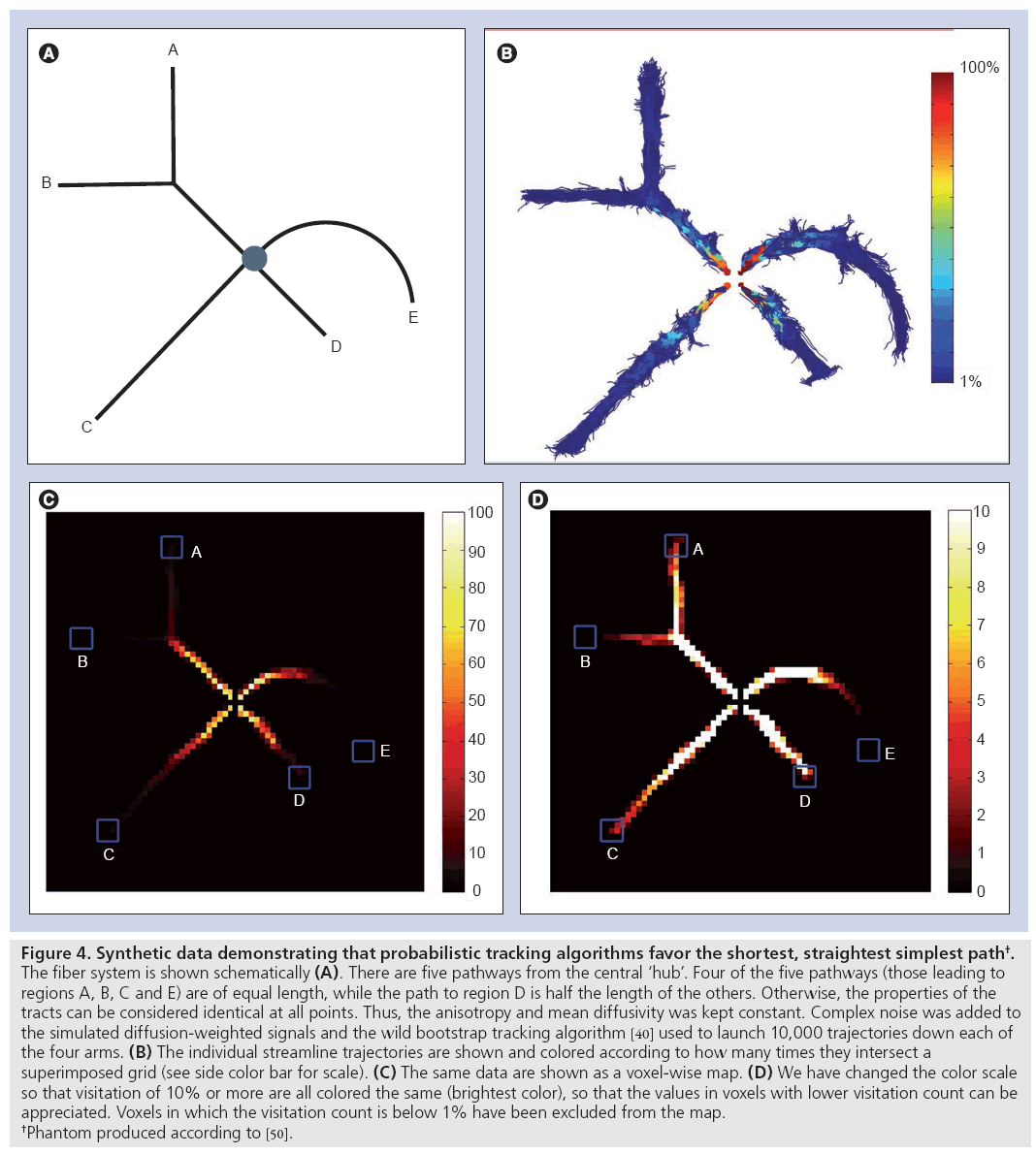
To illustrate all these points, consider a synthetic case with a fiber tract configuration of the form given in Figure 4A, in which the properties of the white matter can be considered to be completely uniform (the same number of axons, same diameter distribution, same degree of myelination and same membrane permeability). Thus, all parts of this network will have exactly the same structural ‘connectivity’ according to both definitions (i.e., in terms of the number of axonal projections at any point, and the microstructural attributes and, therefore, the capacity to convey information). However, as demonstrated in Figure 4B, the number of streamlines reaching the end of the respective branches in the phantom is highly variable. Figure 4C shows the same data presented in the usual manner of mapping the number of voxel intersections. Given that it is difficult to ascertain the number of streamlines reaching the ends of the tracts, a different mapping has been used for Figure 4D, which has had all voxels with a visitation count below 1% excluded.

Figure 4: Synthetic data demonstrating that probabilistic tracking algorithms favor the shortest, straightest simplest path†. The fiber system is shown schematically (A). There are five pathways from the central ‘hub’. Four of the five pathways (those leading to regions A, B, C and E) are of equal length, while the path to region D is half the length of the others. Otherwise, the properties of the tracts can be considered identical at all points. Thus, the anisotropy and mean diffusivity was kept constant. Complex noise was added to the simulated diffusion-weighted signals and the wild bootstrap tracking algorithm [40] used to launch 10,000 trajectories down each of the four arms. (B) The individual streamline trajectories are shown and colored according to how many times they intersect a superimposed grid (see side color bar for scale). (C) The same data are shown as a voxel-wise map. (D) We have changed the color scale so that visitation of 10% or more are all colored the same (brightest color), so that the values in voxels with lower visitation count can be appreciated. Voxels in which the visitation count is below 1% have been excluded from the map.
†Phantom produced according to [50].

Several observations are striking. Even at a threshold of 1%, it can be argued that points B and E are not connected to the central hub. In terms of ‘connection strength’, the five regions can be ranked as D, C, A, B and E. Thus, the algorithm has determined that the two points with the highest ‘connectivity’ are those points that are connected by the shortest, straightest and simplest path.

To emphasize this concept, consider the long path that runs between the central hub and region C. Consider a point midway between the hub and point C (and call it ‘M’), it is clear that M is more strongly connected to the hub than it is to point C, and is more strongly connected to the hub than point C itself. However, these are two points along exactly the same path where the total number of axonal connections, the anisotropy and all other parameters remain constant. How can ‘connectivity’ vary along the same anatomical pathway? This simple cartoon example speaks volumes about the limits of the technique to quantify anatomical connectivity.

Of course, only the differences in quantitative metrics of connectivity that arise owing to different topologies/path lengths within the same brain have been considered here. Needless to say, in group comparisons, where inter-individual differences in brain dimensions exist – or in patient-control comparisons, where the dimensions of the brain in the patient group may be altered by atrophy, tumors and cysts – interpretation will be even more difficult. A heavily atrophied brain, for example, has shorter distances between nodes than a healthy brain. However, it is possible that the quantitative metric of connectivity could become higher in the atrophied brain than in the healthy brain.

Fiber count: a measure of connection strength?

An alternative approach that has been employed in the literature to look for group differences, asymmetries or structure–function correlations is to use the concept of ‘fiber count’ derived from deterministic tracking. This approach counts the number of streamlines that can be reconstructed between two regions of interest. In many ways, this approach is similar to probabilistic tracking, but rather than determining how reproducibly a path can be reconstructed from a single voxel to another voxel, the ‘fiber-count’ approach determines how frequently a streamline can be reconstructed from a collection of voxels in one region of interest to a collection of voxels in another. It should now be clear that exactly the same problems that plague probabilistic tractography will be an issue in the fiber count approach, which will also favor the shortest, straightest and simplest paths and, thus, also produce very biased measurements. In the deterministic approach, it is important to consider the reasons why a streamline would not pass between the two regions of interest:

▪ There is genuinely no anatomical pathway between these regions

▪ The uncertainty in the estimations of fiber orientation is such that the errors accumulate and drive the streamline off course

▪ The streamline propagation is terminated by certain termination criteria

With regard to the second point, it is important to remember that the uncertainty in fiber orientation depends on anisotropy (in a nonlinear fashion [35]). Consequently, a white matter bundle with higher anisotropy will naturally exhibit a higher ‘fiber count’ than a bundle with lower anisotropy – even if the topologies of the two pathways are identical, so the ‘fiber count’ becomes biased. With regard to the third reason, typical termination criteria are usually: to stop tracking when the anisotropy drops below a given threshold and/or to stop tracking when the angle turned between successive steps exceeds a given threshold. Many groups only employ the former criterion and it is easy to see, therefore, that alterations in anisotropy alone can modify the fiber count, even if the associated uncertainty in fiber orientation was kept constant.

It should be noted that attempts have been made to correct the problem of longer tracts having greater accumulated error and, therefore, lower apparent connectivity [43,44]. For example, Tomassini et al. took the summed length of the reconstructed streamlines as a measure of connectivity. While they obtained useful results [44], the correction for tract length is only approximate, and does not differentiate between curved and straight lines that have the same arc length. Such adjustments to connectivity metrics are rarely employed and, to date, existing solutions to the problem are incomplete.

‘Spatial extent’ of connections

Another approach adopted in the literature to assess differences in connectivity is to consider the spatial extent of the connectivity pattern. One approach has been to consider the number of voxels intersected by streamlines (resulting either from deterministic or probabilistic tracking approaches) and, if this is higher, it is concluded that there is more ‘extensive’ connectivity in that region. There are several shortcomings in this approach. First, each reconstructed ‘streamline’ is infinitesimally thin and simply represents the loci of connected points formed by following discrete estimates of fiber orientation. As such, a collection of streamlines has no ‘width’ per se. The approach usually adopted is to identify which voxels are intersected by a streamline. This mapping instantly assigns a volume (in multiples of voxel volume) to the streamline. The more spread out the streamlines are, the larger the number of voxels and, therefore, the larger the volume occupied by the ‘tracts’. The problem here is that uncertainty in fiber orientation scales anisotropy. In regions of low anisotropy, there is a greater uncertainty – and, thus, there will be a greater spread in the streamlines – and a more extensive volume of ‘connections’. It is useful to consider two ends of the spectrum; a tracking result in an isotropic medium, such as a pot of water, and in a perfectly anisotropic system, such as a liquid crystal with displacements constrained along one axis only. In the former, there is large uncertainty in fiber orientation, and, thus, the tracking result will spread out rapidly creating a large ‘connective’ volume. In the latter, a tightly constrained pathway is traced out and, thus, very few voxels would be intersected. Therefore, the spatial extent of a connectivity pattern resulting from tractography (regardless of whether it is deterministic or probabilistic) is a misleading parameter and its use to make inferences on differential patterns of connectivity should be avoided.

Afferents/efferents & the noncommutative nature of tractography

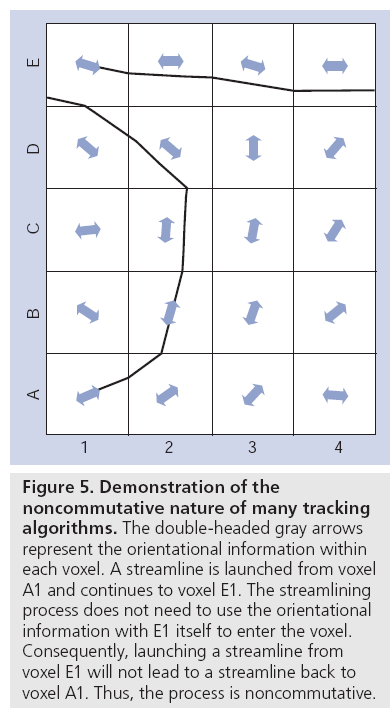
One continued limitation of diffusion MRI is that it cannot currently differentiate between afferent or efferent pathways, since the diffusion of water itself is a symmetrical property. In other words, the probability of a water molecule diffusing a certain distance along a vector +r is exactly the same as the probability of displacing the same distance along vector -r. This is well known, documented and seemingly well understood in the community. What appears to be less well understood is that most fiber tracking algorithms are noncommutative (i.e., when tracking from region A to region B, it cannot be guaranteed that there will be a path back to region A if launching from the ‘target voxels’ in B). This is because in the majority of tractography algorithms, the path goes from location 1 to location n + 1 to location n + 2 and so on. To reach voxel N + n, the chain of the streamline has X ‘knots’ in it (including the start point and end point), but the reconstruction only required X – 1 estimates of the tangent to the curve. To complete the reconstruction to position X, the algorithm does not care what the fiber orientation is at that end point. It just needs to reach it. Consequently, when tracking ‘backwards’ from the end point, unless the fiber is completely straight, the same tracking result will never be obtained (Figure 5).

Figure 5: Demonstration of the noncommutative nature of many tracking algorithms. The double-headed gray arrows represent the orientational information within each voxel. A streamline is launched from voxel A1 and continues to voxel E1. The streamlining process does not need to use the orientational information with E1 itself to enter the voxel. Consequently, launching a streamline from voxel E1 will not lead to a streamline back to voxel A1. Thus, the process is noncommutative.

Again, this speaks volumes about the fact that tractography reveals a path through the data that may not necessarily conform to underlying anatomy.

Where do we go from here?

Not only do we want to establish whether there is a structural remnant of the tissue that is sufficiently ordered to permit a tracking algorithm to assign a tangent to the space curve, but we also need to know whether that tissue is capable of carrying information between the two regions. Therefore, I would like to postulate that not only a measure of the reproducibility of the tangent to the curve and summation of the uncertainty in fiber orientation, but also hard physical attributes of the tract itself are needed.

Imagine that you call an electrician to identify a problem with electrical circuits in your home. He visually inspects the insulated wires and ascertains that the wires follow the continuous paths from room to room, and connect to the appropriate sockets/points. If the electrician does not inspect the integrity of the wiring beneath the plastic coating or the integrity of the connection points, then it is unlikely that he will be able to diagnose the problem fully. Anyone experienced in stringing lights onto a tree for the festive period, only to find that they do not light up when connected to the power socket, will fully appreciate what it is to have a system that is fully connected physically, but lacks the ability to carry ‘information’ along its entire length.

Now consider two tin cans, each with a hole in the bottom and connected by a long piece of string. At all times, there is a very definite (and deterministic) connection between the two tin cans. If the string is taught, then the arrangement can be utilized as a rudimentary telephone and messages passed between the two tin cans. However, if the ‘receiver’ and ‘operator’ walk towards each other, such that the connecting string hangs loose in a parabolic form, the two users are no longer able to communicate with each other – despite the fact that the connectivity, as defined by a ‘streamline’ passing between them, – has not changed (nor has the path length). The thing that has changed is the ability of the string to carry acoustical information along its length. We may boost the number of streamlines extensively (add more strings), but still no useful information can be passed along.

These analogies are useful since they demonstrate that having information simply about the orientation of a path (via the tangent to the curve) is insufficient to determine the potential to carry information. One might even paraphrase Crick and Jones’ paper [6] by referring to the “backwardness of connectional anatomy” and saying that the “microstructural attributes” of the white matter must be known in detail. (“To interpret the activity of living human brains, their neuroanatomy must be known in detail. New techniques to do this are urgently needed, since most of the methods now used on monkeys cannot be used on humans”.) Certainly, diffusion imaging fiber tracking methods have gone some way towards this end but not far enough. However, there has been promising progression; for example, it has been recently demonstrated that quantitative information about axon diameter distribution can be extracted in vivo [20], and methods for mapping the myelination of white matter are continuing to improve [21–23]. By combining information regarding the physical microstructure of the white matter, and improved biophysical models that relate the capability of a fiber to allow information to pass along it to the microstructure, the assessment of brain connectivity in vivo will continue to improve. I do not see it improving by simply considering the orientational information present in the diffusion signal alone.

Conclusion

This article has discussed the motivation for using diffusion MRI as a tool for quantifying connectivity in the brain and suggested different aspects of connectivity that we may wish to target. It then discussed the issues surrounding access to such information and the challenges to be overcome if diffusion MRI is to be used reliably in this context. Some readers might view this article as being a bit pessimistic, especially if it challenges them to reconsider the conclusions of their previous or current work. However, I do not regard it as pessimistic, but realistic, in that it presents many issues that are often ignored/neglected, which might be regarded as very ‘inconvenient truths’. This article serves to redress the balance in some parts of the field concerning the exciting and increasingly ambitious claims made in favor of diffusion MRI.

Part of the issue is the increasing availability of push-button software packages to generate a tract reconstruction from any point in the brain. We have moved from an era, at the transition of the new millennium, where groups were cautiously constructing tracking algorithms – obsessively refining them for use in their own laboratories – to a situation where people who have never studied the physics and limitations of diffusion MRI are now free to click on a voxel and launch fibers. I am sure that there is no intentional denial of the limitations on the part of such users, rather a lack of time to have studied the literature. In friendly discussion, there is often a genuine element of surprise when the limitations, pitfalls and confounds are highlighted. Another part of the issue is the spin put out by the developers of such methods. Results are trumpeted at conferences as the ‘next big thing’ in mapping brain connectivity, only to hear the same groups back-peddle quickly on the limitations of their ‘old’ approach several months later. This is understandable – it is the nature of science and progression – but the back-peddling is not always documented and widely published for all to see. This article is not intended to be a personal attack on particular laboratories. I am certainly no more ‘holier than thou’ and have already confessed to authoring an abstract at the International Society for Magnetic Resonance in Medicine (ISMRM) in 1998 entitled ‘Noninvasive assessment of axonal connectivity’ [45]. So what is the answer? Possibly more education is needed in terms of articles discussing not only the latest and greatest stunning examples of what diffusion MRI can do, but also high profile articles that highlight the limitations [46,47] would be equally important and effective for progressing neuroscience. However, perhaps we need to think beyond diffusion in terms of characterizing connectivity.

Future perspective

As previously alluded to, it is my belief and that of several of my European colleagues that form part of the Consortium of Neuroimagers for the Noninvasive Assessment of Brain Connectivity and Tracts (CONNECT) team (funded by the European Commission under Framework Package 7) that integrating other measures of white matter attributes, including measures of axon density, axon caliber and myelination, with the orientational information present in the diffusion signal, is going to be necessary for progress in characterizing white matter connectivity. For example, one might speculate greater efficiency of information transfer between two regions if there are bigger, fatter axons. The AxCaliber framework [20], or variants thereof, can give insights into distributions of axon diameters. Similarly, since conduction velocity increases with myelination, one may expect higher reaction times and/or higher fidelity of synchronization of activity in different brain regions if the pathways connecting them are more myelinated. Techniques based on magnetization transfer (e.g., [21]) or multicomponent relaxometry (e.g., [22,23]) can provide putative markers of myelination that complement the information provided by diffusion MRI. It is early days for these methods, so one can, at this stage, only speculate as to their usefulness in adding to the assessment of brain connectivity. However, there is a caveat that even if we improved the modeling to fully characterize everything regarding the structural aspects of the white matter, we would not fully capture the connectivity between two regions. Just because a connection exists, it will not necessarily always be engaged during a particular process. As discussed by Stephan et al., the functional connectivity of a network is only constrained, but not fully determined by, its anatomical connections [48]. Thus, a comprehensive assessment of brain connectivity in vivo will necessitate a multimodality approach encompassing a range of techniques to combine dynamical measures of brain activity (oscillations and fluctuations) with multivariate assessment of white matter micro- and macrostructure. Combining these emerging multimodal techniques in the coming years will truly advance our understanding of the connectivity of the brain.

Acknowledgements

The author is extremely grateful to A Leemans for generating the synthetic diffusion data to match the ‘sketch’ in Figure 4A that allowed the author to produce some of the key points of this paper. The author wishes to thank Richard Wise for proofreading the manuscript and to the anonymous reviewers for their helpful comments.

Financial & competing interests disclosure

The author has no relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript. This includes employment, consultancies, honoraria, stock ownership or options, expert testimony, grants or patents received or pending, or royalties.

No writing assistance was utilized in the production of this manuscript.

Ethical conduct

The data used in Figures 1, 2 & 3 were acquired under informed consent and the study protocol was approved by the local (Cardiff School of Psychology, Cardiff University, UK) Ethics Committee.

References

1. Fox MD, Raichle ME: Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 8(9), 700–711 (2007).
2. Smith SM, Fox PT, Miller KL et al.: Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl Acad. Sci. USA 106(31), 13040–13045 (2009).
3. Fox MD, Snyder AZ, Vincent JL, Raichle ME: Intrinsic fluctuations within cortical systems account for inter-trial variability in human behavior. Neuron 56(1), 171–184 (2007).
4. Friston KJ, Harrison L, Penny W: Dynamic causal modeling. Neuroimage 19, 1273–1302 (2003).
5. Mesulam MM: Preface. In: Fiber Pathways Of The Brain. Schmahmann JD, Pandya DN (Eds). Oxford University Press, NY, USA (2006).
6. Crick F, Jones E: The backwardness of human neuroanatomy. Nature 361, 109–110 (1993).

• • Indicates how little is known about human neuroanatomy and highlights the need for new techniques to be developed, since the invasive tracer methods that are used in monkey brains cannot be used in humans. In a way, this article foretold the invention of diffusion MRI and tractography.

7. Bammer R, Holdsworth SJ, Veldhuis WB, Skare ST: New methods in diffusionweighted and diffusion tensor imaging. Magn. Reson. Imaging Clin. N. Am. 17(2), 175–204 (2009).
8. Johansen-Berg H, Rushworth MF: Using diffusion imaging to study human connectional anatomy. Annu. Rev. Neurosci. 32, 75–94 (2009).
9. Mukherjee P, Berman JI, Chung SW, Hess CP, Henry RG: Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am. J. Neuroradiol. 29(4), 632–641 (2009).
10. Neil JJ: Diffusion imaging concepts for clinicians. J. Magn. Reson. Imaging 27(1), 1–7 (2008).
11. Jones DK: Studying connections in the living human brain with diffusion MRI. Cortex 44(8), 936–952 (2008).
12. Mori S (Ed.). Introduction to Diffusion Tensor Imaging. Elsevier, Amsterdam, The Netherlands (2007).

• • Reference book on the topic of diffusion MRI, provides detailed insights into the theory and practice of diffusion MRI, covering far more material than can be covered here.

13. Johansen-Berg H, Behrens TEJ (Eds). Diffusion MRI: From Quantitative Measurement to In-Vivo Neuroanatomy. Elsevier, Amsterdam, The Netherlands (2009).

• • Reference book on the topic of diffusion MRI, provides detailed insights into the theory and practice of diffusion MRI, covering far more material than can be covered here.

14. Jones DK (Ed.). Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, Oxford, UK (2010).

• • Reference book on the topic of diffusion MRI, provides detailed insights into the theory and practice of diffusion MRI, covering far more material than can be covered here.

15. Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM: Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med. 54, 1377–1386 (2005).
16. Tuch DS: Q-ball imaging. Magn. Reson. Med. 52, 1358–1372 (2004).
17. Tournier J-D, Calamante F, Gadian DG, Connelly A: Direct estimation of the fiber orientation density function from diffusionweighted MRI data using spherical deconvolution. Neuroimage 23, 1176–1185 (2004).
18. Alexander DC: Multiple-fiber reconstruction algorithms for diffusion MRI. Ann. NY Acad. Sci. 1064, 113–133 (2005).
19. Assaf Y, Basser PJ: Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage 27, 48–58 (2005).
20. Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ: AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn. Reson. Med. 59(6), 1347–1354 (2008).
21. Cercignani M, Symms MR, Schmierer K et al.: Three-dimensional quantitative magnetisation transfer imaging of the human brain. Neuroimage 27, 436–441 (2005).
22. Deoni SCL, Rutt BK, Pierpaoli C, Jones DK: Gleaning multi-component T1 and T2 information from steady-state imaging data. Magn. Reson. Med. 60, 1372–1387 (2008).
23. Deoni SC, Rutt BK, Aruna T, Pierpaoli C, Jones DK: Whole-Brain Myelin Imaging Through Multi-Component Analysis of Steady-State Imaging Data. Organization for Human Brain Mapping, Melbourne, Australia 269 (2008).
24. Jones DK, Simmons A, Williams SCR, Horsfield MA: Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magn. Reson. Med. 42, 37–41 (1999).
25. Buchsbaum MS, Tang CY, Peled S et al.: MRI white matter diffusion anisotropy and PET metabolic rate in schizophrenia. Neuroreport 9(3), 425–430 (1998).
26. Friston KJ, Frith CD: Schizophrenia: a disconnection syndrome? Clin. Neurosci. 3(2), 89–97 (1995).
27. Beaulieu C: The basis of anisotropic water diffusion in the nervous system – a technical review. NMR Biomed. 15(7–8), 435–455 (2002).
28. Pierpaoli C, Jezzard P, Basser PJ, Barnett A, di Chiro G: Diffusion tensor MR imaging of the human brain. Radiology 201(3), 637–648 (1996).
29. Tuch DS, Salat DH, Wisco JJ, Zaleta AK, Hevelone ND, Rosas HD: Choice reaction time performance correlates with diffusion anisotropy in white matter pathways supporting visuospatial attention. Proc. Natl Acad. Sci. USA 102(34), 12212–12217 (2005).
30. Mori S, Crain BJ, Chacko VP, Van Zijl PC: Three dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 45, 265–269 (1999).
31. Conturo TE, Lori NF, Cull TS et al.: Tracking neuronal fiber pathways in the living human brain. Proc. Natl Acad. Sci. USA 96, 10422–10427 (1999).
32. Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A: In vivo tractography using DT-MRI data. Magn. Reson. Med. 44, 625–632 (2000).
33. Catani M, Howard RJ, Pajevic S, Jones DK: Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 17, 77–94 (2002).
34. Kinoshita M, Yamada K, Hashimoto N et al.: Fiber tracking does not accurately estimate size of fiber bundle in pathological condition: initial neurosurgical experience using neuronavigation and subcortical white matter stimulation. Neuroimage 25(2), 424–429 (2005).

• Surprising in its honesty, in discussing what went wrong when information provided by diffusion MRI tractography was used in neurosurgical planning.

35. Jones DK: Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn. Reson. Med. 49, 7–12 (2003).
36. Koch M, Glauche V, Finsterbusch J, Nolte U, Frahm J, Buchel C: Estimation of anatomical connectivity from diffusion tensor data. Neuroimage 13, S176 (2001).
37. Koch MA, Norris DG, Hund-Georgiadis M: An investigation of functional and anatomical connectivity using magnetic resonance. Neuroimage 16, 241–250 (2002).
38. Parker GJ, Haroon HA, Wheeler-KingshottCA: A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J. Magn. Reson. Imaging. 18(2), 242–254 (2003).
39. Jones DK, Pierpaoli C: Confidence mapping in deterministic DT-MRI tractography. Magn. Reson. Med. 53, 1143–1149 (2005).
40. Jones DK: Tractography gone wild: probabilistic fiber tracking using the wild bootstrap with diffusion tensor MRI. IEEE Trans. Med. Imaging 27, 1268–1274 (2008).
41. Behrens TE, Johansen-Berg H, Woolrich MW et al.: Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat. Neurosci. 6(7), 750–757 (2003).

• • Used probabilistic tractography to identify which parts of the cortex different parts of the thalamus were most likely to connect to, and to segment the thalamus. Despite the challenges and limitations outlined in this article, the authors were able to obtain a good segmentation. Do note, however, that this method does not depend on quantification of connectivity per se in order to work.

42. Pierpaoli C, Barnett A, Pajevic S et al.: Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage 13, 1174–1185 (2001).
43. Morris DM, Embleton KV, Parker GJ: Probabilistic fiber tracking: differentiation of connections from chance events. Neuroimage 42, 1329–1339 (2008).

• Discusses the ‘distance normalization’ problem associated with probabilistic fiber tracking. Although it does not provide a complete solution, it discusses the issue in some depth.

44. Tomassini V, Jbabdi S, Klein JC et al.: Diffusion-weighted imaging tractographybased parcellation of the human lateral premotor cortex identifies dorsal and ventral subregions with anatomical and functional specializations. J. Neurosci. 27(38), 10259–10269 (2007).
45. Jones DK, Simmons A, Williams SCR, Horsfield MA: Non-invasive assessment of structural connectivity in white matter by diffusion tensor MRI. Proceedings of ISMRM 6th Annual Meeting. Sydney, Australia 531 (1998).
46. Le Bihan D, Poupon C, Amadon A, Lethimonnier F: Artifacts and pitfalls in diffusion MRI. J. Magn. Reson. Imaging 24(3), 478–488 (2006).
47. Jones DK, Cercignani M: 25 pitfalls in the analysis of diffusion MRI data. NMR Biomed. (2010) (In Press).

• • Discusses many practical issues to be considered when embarking on a diffusion MRI-based study.

48. Stephan KE, Tittgemeyer M, Knösche TR, Moran RJ, Friston KJ: Tractography-based priors for dynamic causal models. Neuroimage 47, 1628–1638 (2009).
49. Leemans A, Jeurissen B, Sijbers J, Jones DK: ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data. Presented at: ISMRM 17th Annual Meeting. Honolulu, Hawaii, 18–24 April 2009.
50. Leemans A, Sijbers J, Verhoye M, Van der Linden A, Van Dyck D: Mathematical framework for simulating diffusion tensor MR neural fiber bundles. Magn. Reson. Med. 53(4), 944–953 (2005).