Research Article - Imaging in Medicine (2017) Volume 9, Issue 4
Spatial intuitionistic fuzzy set based image segmentation
Deepika Koundal*, Bhisham Sharma & Ekta GandotraDepartment of Computer Science & Engineering, Chitkara University, Rajpura, India
- Corresponding Author:
- Deepika Koundal
Department of Computer Science & Engineering
Chitkara University, Rajpura, India
E-mail: deepika.koundal@chitkara.edu.in
Abstract
Segmentation of images is one of the most challenging tasks because of restricted observation of the specialists and uncertainties presented in medical knowledge. Crisp values are inadequate to model real situation due to imprecise information frequently used in decision making process. Various intuitive methods have been explored to understand the ambiguity and uncertainty of medical images to carry out segmentation task. Therefore, in this paper, an attempt has been made to segment the medical images using clustering method based on Intuitionistic fuzzy set. With the incorporation of spatial information into intuitionistic clustering named as Spatial Intuitionistic Fuzzy C Means (SIFCM), the object of interest is segmented more accurately and effectively. The benefits of incorporating spatial information is that it is a powerful method for noisy image segmentation and works for both single and multiple-feature data with spatial information as well as capable of reduction of noisy spots and spurious blobs. The performances of proposed methods are evaluated for real images. The results indicate that SIFCM is more effective, and noise tolerant as compared with the fuzzy c-means clustering.
Keywords
spatial information ▪ clustering ▪ intuitionistic ▪ fuzzy, image segmentation
Introduction
Clustering is one of the unsupervised segmentation methods for the partitioning of image into different parts having some homogeneous features. Uncertain information is presented in medical images due impreciseness and fuzziness of pixels and edges [1]. However, due to the uncertainty and complexity of images, clustering is commonly used to segment the images into different clusters having similar pixel values [1-6].
In 1965, Zadeh has given the concept of Fuzzy Sets (FS) for handling uncertainty in medical images [1]. FS utilizes the ambiguity in mathematical form. It is used as a powerful tool to deal with the uncertainty and fuzziness presented in images. Fuzzy clustering is obtained by minimizing the cost function iteratively which is based on the pixels distance to the cluster centers. However, it can only handle the membership degree and fails to handle non-membership and indeterminacy degree of imprecise parameters. Other limitations such as noisy pixels are misclassified due to its imprecise feature information. Therefore, generalization of FS in form of Intuitionistic Fuzzy Set (IFS) is becoming more popular in image processing in order to overcome the limitations of fuzzy based approaches.
One major drawback of Fuzzy clustering is that it does not taken into account the spatial context of the pixels as it is sensitive to artifacts and noise. Therefore, some attempts have been made by number of authors to incorporate spatial information into fuzzy clustering. Chuang et al. introduced a Fuzzy C-Means (FCM) method that incorporates spatial information into the membership function for clustering [2]. Wang et al. presented a fuzzy segmentation scheme by utilizing local contextual information and the high inter-pixel correlation inherent. In these, the initial center of cluster as well as membership function is determined adaptively based on local spatial similarity measure model [7]. Cai et al. proposed a fast and robust fuzzy framework for image segmentation by incorporating local spatial and gray level information together [8].
Atanassov [9] presented the concept of Intuitionistic Fuzzy Set (IFS), which is more practical in real situations. It is characterized as membership and non-membership function. IFS is only able to deal uncertain information by membership and non-membership degree but not able to handle indeterminate and imprecise information which commonly exists in belief system. Therefore, researchers have paid more importance to it [10]. In IFSs, total of membership and non-membership degree of imprecise information is less than unity. Hence, certain amount of indeterminacy is not handled by IFS. It cannot handle all types of uncertainties successfully, which involves inadequate information. Although FSs and IFSs are very successful in image segmentation, they cannot deal with the indeterminate and inconsistent information that exists in real problems. Therefore, further generalizations of FS and IFS are required. However, the limitation is that diffused edges of object of interest cannot be properly segmented from surrounding tissues in medical image. The neighboring pixels in the immediate neighborhood possess similar feature values, which is an important characteristic that can be of great aid in clustering.
Though numbers of image clustering methods have been presented but spatial information is not often widely considered. As there is no work in the literature on IFCM clustering incorporating spatial information, therefore, to show its efficacy, various experiments are carried out to segment the medical images. In this paper, an attempt has been made to propose an IFCM clustering incorporating spatial information for image segmentation. The method incorporates spatial information with uncertainty and indeterminacy that arises while defining the membership function. As few work has been based on the incorporation of spatial information into Intutionistic fuzzy set [11,12]. In these, the objective function is modified according to IFCM. Then, the cluster center is updated using IFCM with the incorporation of an objective function i.e. the spatial information in the criterion function. Experimental results show that the proposed methods achieve better segmentation results in comparison to other clustering methods.
The rest of this paper is organized in five sections. Section 2 describes the material and methods. Clustering with spatial information is given in section 3. Section 4 consists of experimental results. Finally, the conclusion and discussion is summarized in Section 5.
Material and methods
■ Material
To validate the proposed method, experiments are performed on the open access database of ultrasound images available at the website of computer imaging & medical applications Laboratory, Universidad Nacional de Colombia [13]. It consists of total 88 thyroid US images. An experienced radiologist outlines every lesion and the manual delineation served as reference. For evaluating the performance of proposed clustering method and its quantitative comparison, cluster validity functions such as fuzzy partition and feature structure are used [14]. The representative functions for the fuzzy partition are Partition Coefficient (PC) and Partition Entropy (PE). Partition Coefficient (PC) quantifies the closeness of all pixels to their corresponding cluster centers. It can be defined as
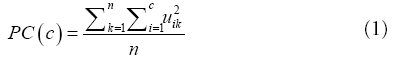
Where 1/C ≤ PC ≤ 1, u is the membership value, c is number of cluster. The value of PC lies is in the range [1/C, 1] An index of PC=1/C indicates that there is no clustering tendency.
The Partition Entropy (PE) can be expressed as
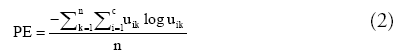
The value of PE is in the range [0, log c]. Both measure the fuzziness degree of partitions. A high index value indicates good cluster separation, while an index value less than 1 indicates fuzzier clustering.
■ Methods
Fuzzy C Means (FCM) clustering: FCM has one real value μA(X) є [0,1], used for the representation of membership degree of fuzzy set A that is defined on the universe of discourse X. The FCM clustering is used to classify image by grouping similar pixels into clusters. A fuzzy set ∼ A can be defined as
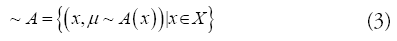
Where μ ∼ A: X -> [0,1]
The FCM clustering minimizes the following objective function:
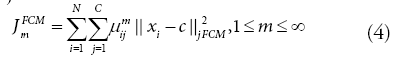
Where m is called the weighting exponent that have influence on the clustering performance of FCM, m>1, μij is the membership of xi in cluster j, xi is the ith datum, cj is the center of cluster j, and ‖. ‖ is any norm expressing the similarity between the datum and the center.


Intuitionistic Fuzzy C Means (IFCM) clustering: Atanassov [9] introduced the Intuitionistic Fuzzy Set (IFS) that is the generalization of FS [4-6]. IFSs act as a tool for making decisions in the presence of inadequate facts and imprecise knowledge. From recent publications, some edge detection and thresholding techniques are presented on medical images using IFS. The IFS based methods have high flexibility and accuracy to many conditions.
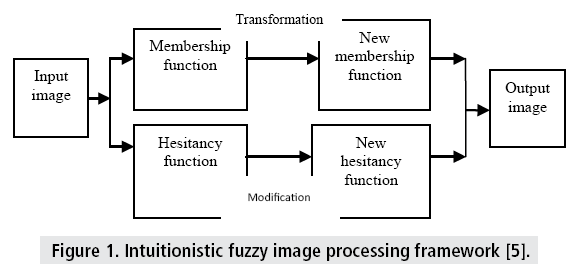
For the application of IFS, the image is transformed into the intuitionistic domain by defining appropriate membership and non- membership functions. After obtaining the membership and hesitance or non-membership functions, their modification is carried out according to the desired image operation. An overview of intuitionistic fuzzy image-processing framework is illustrated in FIGURE 1.
However, the task of describing an image in IFS domain is little bit complicated. The complexity arises due to ambiguity while defining membership function and nonmembership function. Thus, an intuitive method is introduced for image fuzzification that reflected the inherent ambiguity and vagueness carried by the image itself. A IFS A defined on a universe X is represented by
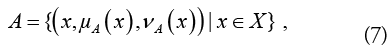
here
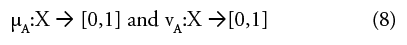
with the condition
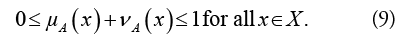
Where μA(x) and vA(x) signify the membership degree and the non-membership degree of x to A respectively.
Furthermore, it takes a third parameter
μA (x) that is known as hesitation degree or intuitionistic fuzzy index for the distance calculation between IFSs [13,15-16]. For IFS, the hesitation degree occurs due to the lack of knowledge in membership degree of each element x in A is defined as:
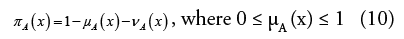
Hence with the hesitation degree, μA(x), an intuitionistic fuzzy subset A in X may be denoted as:
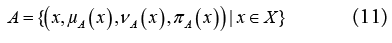
with the condition as 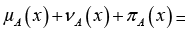 1. It is obvious that 0 ≤ μA(x) ≤ 1 for each x ∈ X.
1. It is obvious that 0 ≤ μA(x) ≤ 1 for each x ∈ X.
The membership, non-membership and hesitation degree must be used to describe an IFS. IFCM clustering is based on the minimization of objective function that contains two terms represented as:
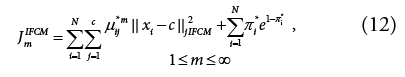
Where 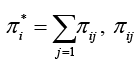 is the hesitation degree,
is the hesitation degree,
m is weighting exponent, μij is the sum of μij and πij known as intuitionistic fuzzy membership of the jth point in the ith cluster [6].
The membership functions μij and center vector cj *are updated iteratively given as
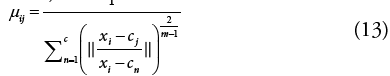

Finally, the membership matrix and cluster center is updated according to the stopping criteria at each iteration.
■ Clustering with spatial information
In conventional clustering, assignment of cluster is exclusively based on the distribution of pixels in the feature space but not on the distribution of pixels in spatial domain. The membership function on the basis of local image feature is proposed to determine the membership and center of cluster adaptively [2,7,8]. The adjoining pixels of an image are extremely correlated to each other and the probability of belongingness to the same cluster is high due to their identical feature values. However, the neutrosophic clustering and intuitionistic clustering considered the numerical features of pixels and neglected the general spatial correlation. In this paper, the local image feature is incorporated for modifying the membership function [7]. For the exploitation of local image feature, a spatial function is defined as

Where Nn signifies a pixels belonging to the window centered around the pixel n in a spatial fuzzy domain. The size of window is taken as 5. The weighted ujk and the centroids c are updated iteratively. Just like the membership function, the spatial function hij represents the probability that pixel xj belongs to ith cluster.
Neighboring pixels of an image are highly correlated to each other. The spatial function of a pixel for a cluster is considerable if most of the neighborhood pixels belong to the same cluster. This type of correlation is also known as spatial relationship in clustering. In this method, spatial information of neighboring pixels are incorporated into fuzzy membership directly using
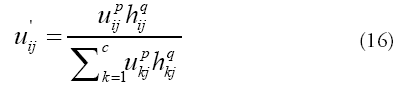
where p and q are the two parameters controlling the respective contribution [7].
The spatial functions just strengthen the initial membership function and the result of clustering remains unaffected in the homogenous region. However, for a noisy pixel, this function decreases the influence of a noisy cluster by the labels of its neighboring pixels. So, misclassified pixels from noisy regions or spurious blobs can simply be corrected [14].
The Spatial Intuitionistic Fuzzy C Means (SIFCM) clustering is proposed with the incorporation of local contextual information and the intrinsic inter-pixel correlation. Firstly, the initial cluster center and initial membership function are determined adaptively based on local spatial similarity measure. Then, the fuzzy membership function is modified to compute the spatial function. The fuzzy iteration proceeds with the new membership that is incorporated with the spatial function. The iteration is stopped when the maximum difference between two cluster centers at two successive iterations is less than a threshold. After the convergence, de-fuzzification is applied to assign each pixel to a specific cluster for which the membership is maximal. Finally, the image is segmented by using SIFCM clustering. The algorithm is given below:
Proposed Algorithm: SIFCM
Input: Image f
Output: Segmented region
(a) Carry out the Intuitionistic fuzzy clustering on the given image.
(b) Initialize number of clusters ‘c’, iteration index k=0,εps 1 × 10-5 membership matrix μij and membership parameter ‘m’, where ‘i’ is the cluster index and ‘j’is the pixel index.
(c) Transformation of image into the intuitionistic domain by computing vA(x), μA(x)andπA(x) for the image f[11]
(d) Center vector cj is computed by eq.(14) and the cost function of intuitionistic fuzzy clustering is evaluated.
Update spatial membership function μij by incorporating hij directly into the membership function using Eq.(16).
Stopping criteria given in Eq.(5.15) is used to stop the iteration.
If stopping criteria 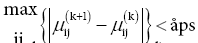 is
satisfied, then stop; else goto step (d).
is
satisfied, then stop; else goto step (d).
comparison is done with FCM, SFCM and IFCM methods. From TABLE 1, it is revealed that the PC and CE values obtained for SFCM is better than the values obtained for FCM. With the incorporation of spatial information, SIFCM provide better results. The parameter m is employed to compute the membership function. In experiments, the values of m are taken between 2 to 5 as shown in TABLE 1. It is observed from the TABLE 1 that effective values are achieved at m=2 as compared to other values of m.
| m=2 | m=3 | m=4 | m=5 | |||||
|---|---|---|---|---|---|---|---|---|
| PC | CE | PC | CE | PC | CE | PC | CE | |
| FCM | 0.868 | 0.375 | 0.693 | 0.609 | 0.873 | 0.365 | 0.822 | 0.332 |
| SFCM | 0.871 | 0.129 | 0.8598 | 0.016 | 0.860 | 0.246 | 0.835 | 0.250 |
| IFCM | 0.912 | 0.478 | 0.909 | 0.283 | 0.618 | 0.171 | 0.875 | 0.519 |
| SIFCM | 0.943 | 0.461 | 0.947 | 0.160 | 0.902 | 0.106 | 0.913 | 0.133 |
Table 1: Comparison of FCM, IFCM, SFCM and SIFCM on thyroid images.
FIGURE 2a shows an original image of vessels and FIGURE 2b shows the ground truth image. The result of FCM (FIGURE 2c) illustrates that the boundaries of vessels are weak and blurry causing boundary leakage problem. It can be observed that the boundaries of vessels and its adjoining tissues are generally frail. From FIGURE 2d, it is observed that the IFCM segmented the vessels but it tends to thinner the vessels from its original size and lower part of the vessel is not properly segmented out. FIGURE 2g shows that vessel is segmented out better with the SFCM incorporating spatial information as compared to FCM. As compared the FIGURES 2d and 2g, it is clear that SIFCM is able to eliminate the unimportant pixels, which are also considered in IFCM.
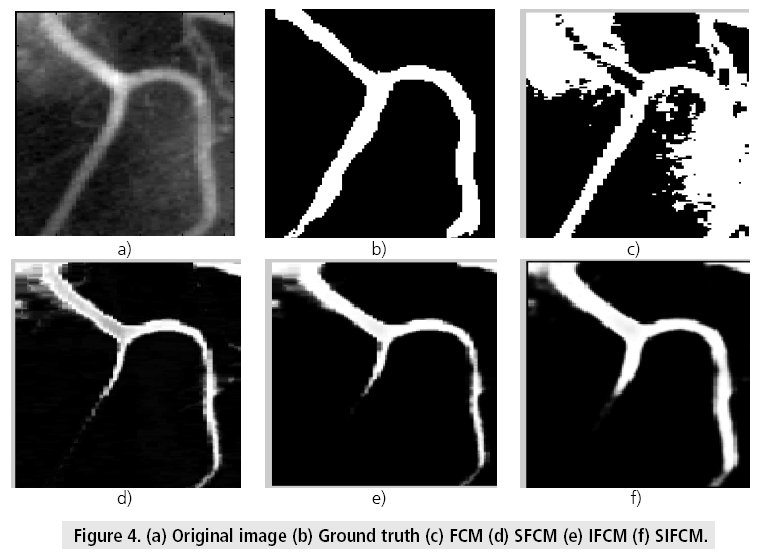
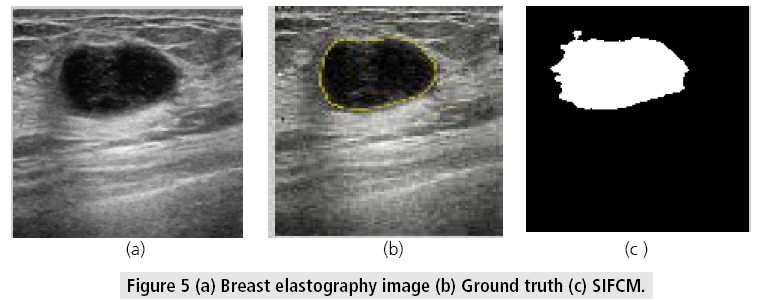
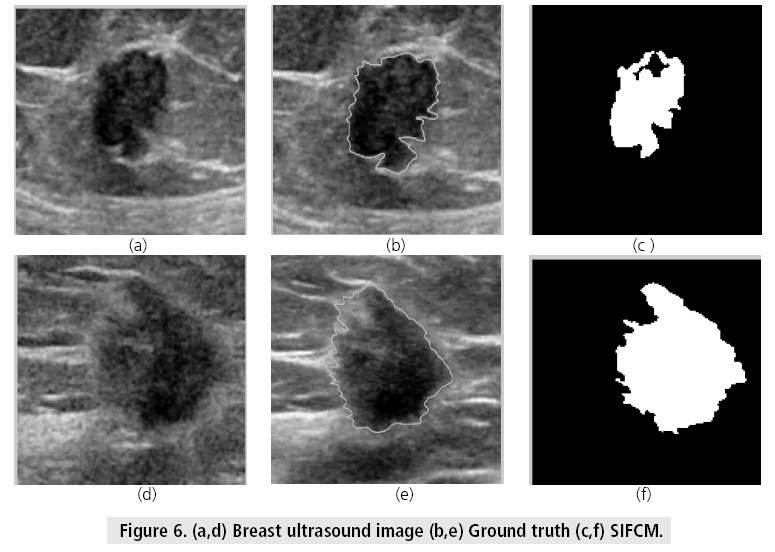
FIGURE 3 illustrates the visual results of all methods. The proposed method is suitable for other medical images also. The generalization of proposed method, the results are shown on other medical images also. The visual results of artery image are shown in FIGURE 4 whereas the results of breast cancer images which are collected from http://www.onlinemedicalimages.com/index.php/en/site-map are shown in FIGURES 5 and 6. The results of SIFCM demonstrate that the segmentation is better than other methods. The result of FCM miss-classify the indeterminate regions into foreground, since it uses only the distance to calculate the cluster centers (membership is based on distance too), without considering the indeterminate degree. SIFCM handles the uncertainity with hesitation degee in defining membership function.
Conclusion
Intuitionistic set provides a powerful tool that can describe the image with uncertain information. This paper provides the efficacy of intuitionistic clustering with spatial information for medical image segmentation. It is observed that the results using SIFCM are much better than the FCM/SFCM because fuzzy set is not able to consider uncertainty as the membership function while IFCM is able to consider uncertainties as hesitation degree and indeterminacy degree while defining membership function respectively. As medical images are of low contrast with vague region or boundaries, SIFCM give better results. Through the work discussed above, shows that Intuitionistic based approaches can find more applications in image processing and pattern recognition. When membership function is not always accurately defined due to the lack of personal error, IFS may help in solving the problem. Our ongoing and further works include clustering validity in our methods, adaptive determination for the clustering number and other applications.
References
- Zadeh LA. Fuzzy sets. Information. and. Control. 8, 338-353 (1965).
- Chuang K, Tzeng H, Chen S et al. Fuzzy c-means clustering with spatial information for image segmentation. Comput. Med. Imaging. Graph. 30, 9-15 (2006).
- Atanassov K. More on intuitionistic fuzzy sets. Fuzzy. Sets. and. Systems. 33, 37-46 (1989).
- Wang H, Madiraju P, Zhang Y et al. Interval neutrosophic sets. International. Journal. of. Applied. Mathematics. and. Statistics. 3, 1-18 (2005).
- Chaira T. Intuitionistic fuzzy set: Application to medical image segmentation. Studies. in. Computational. Intelligence. 85, 51-68 (2008).
- Chaira T, Ray AK. A new measure using intuitionistic fuzzy set theory and its application to edge detection. Appl. Soft. Comput. 8, 919-927 (2008).
- Wang X, Bu J. A fast and robust image segmentation using FCM with spatial information. Digital. Signal. Processing. 20, 1173-1182 (2010).
- Cai W, Chen S, Zhang D. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern. Recognit. 40, 825-838 (2007).
- Atanassov K. Intuitionistic fuzzy sets. Fuzzy. Sets. and. Systems. 20, 87-96 (1986).
- Bhowmik M, Pal M. Intuitionistic neutrosophic set. Journal. of. Information. and. Computing. Science. 4, 142-152 (2009).
- Tripathy BK, Basu A, Govel S. Image segmentation using spatial intuitionistic fuzzy c means clustering. In Computational Intelligence and Computing Research (ICCIC). IEEE International. Conference. 1-5 (2014).
- Verma H, Agrawal RK, Sharan A. An improved intuitionistic fuzzy c-means clustering algorithm incorporating local information for brain image segmentation. Appl. Soft. Comput. 46, 543-557 (2016).
- http://cimlaboratory.com
- Chaira T. Intuitionistic fuzzy segmentation of medical images. IEEE. Trans. Biomed. Eng. 57, 1430-1436 (2010).
- Hung KC. Medical pattern recognition: Applying an improved intuitionistic fuzzy cross-entropy approach. Advances. in. Fuzzy. Systems. 1 (2012).
- Chaira T. Intuitionistic fuzzy set theory in medical imaging. Int. J. Soft. Comput. Eng. 1 (2011).