Review Article - Journal of Experimental Stroke & Translational Medicine (2010) Volume 3, Issue 1
Towards a dynamical network view of brain ischemia and reperfusion. Part I: background and preliminaries
- *Corresponding Author:
- Donald J. DeGracia, Ph.D.
Department of Physiology, Wayne State University, 4116 Scott Hall
540 East Canfield Ave., Detroit, MI 48201, U.S.A
Phone: 313-577-6745
Fax 313-577-5494
E-mail: ddegraci@med.wayne.edu.
Abstract
The general failure of neuroprotectants in clinical trials of ischemic stroke points to the possibility of a fundamen-tal blind spot in the current conception of ischemic brain injury, the “ischemic cascade”. This is the first in a se-ries of four papers whose purpose is to work towards a revision of the concept of brain ischemia by applying network concepts to develop a bistable model of brain ischemia. This first paper sets the stage for developing the bistable model of brain ischemia. Necessary background in network theory is introduced using examples from developmental biology which, perhaps surprisingly, can be adapted to brain ischemia with only minor mod-ification. Then, to move towards a network model, we extract two core generalizations about brain ischemia from the mass of empirical data. First, we conclude that all changes induced in the brain by ischemia can be classified as either damage mechanisms that contribute to cell death, or stress responses that contribute to cell survival. Second, we move towards formalizing the idea of the “amount of ischemia”, I, as a continuous, non-negative, monotonically increasing quantity. These two generalizations are necessary precursors to reformulat-ing brain ischemia as a bistable network.
Keywords
Boolean networks; brain ischemia and reperfusion; focal cerebral ischemia; global cerebral ischemia; neuroprotection
Abbreviations
CBF cerebral blood flow
DMSO dimethly sulfoxide
GEDI gene expression dynamics inspector
MCAO middle cerebral artery occlusion
ROS reactive oxygen species
STAIR stroke therapy academic industry roundtable
UPR unfolded protein response
Puzzle pieces
The general failure of neuroprotection in stroke clini-cal trials has put the field in a relative state of crisis. But crisis is another word for opportunity and the sit-uation has generated much activity. These activities have largely been directed towards further refinement of existing preclinical and clinical methodology as began by the STAIR group (Gladstone et al. 2002; Dirnagl 2006; Fisher et al. 2005; Fisher et al., 2009), or to further pushing back the empirical frontier (En-dres et al 2008). These are clearly important goals. Additional possibilities were offered by O’Collins et al (2006) in their well-known review of neuroprotectants, which sets the stage for the present work:
“No particular drug mechanism distinguished itself on the basis of superior efficacy in animal models of foc-al ischemia. This may reflect the multifaceted nature of the sequelae of ischemic stroke and suggest a role for combination therapy to target multiple processes. Alternately, it might suggest that our conception of stroke needs reformulation. A tendency to exclusively frame drug activity in terms of the dominant schema of stroke damage (eg. excitotoxicity, free radical damage), coupled with the sometimes arbitrary attri-bution of a drug mechanism to one of several nonmu-tually exclusive groupings, might distract from other paradigms with greater explanatory power, thus hin-dering the development of more effective treatments.” (p 474)
Although these statements have generated some controversy, there is prescience to them. While the observation that no neuroprotectant has shown supe-rior efficacy to any other is an important empirical clue we focus on in the 3rd paper of this series, here we highlight the authors’ suggestion that we might be looking at the problem incorrectly. Given the urgency of the problem, it is surprising that there has been a relative dearth of effort directed towards the possibili-ty that our conception of stroke may require reformu-lation. There have been efforts along these lines (Lo 2008; Yenari et al 2008), but these are in the quantit-ative minority. Further, such efforts tend to be what Huang (2009) has called “metaphorical” as opposed to approaches that are formal or systematic.
More broadly speaking, since stoke is an example of focal brain ischemia, it is natural to expand the con-clusion of O’Collins et al to brain ischemia as a whole. Is it possible to reformulate what it means for a brain to experience ischemia? Currently, the idea of the “ischemic cascade” dominates our understanding of the phenomena. To use O’Collins et al.’s term, it is the “dominant schema”. But are there alternative possibilities, other “paradigms with greater explanato-ry power” that may aid us in reformulating our under-standing of brain ischemia? In this regard, consider the following statement from Lipton (1999):
“There are three aspects of ischemic cell death which suggest that a formalism that is applied to dynamical systems, in which attractors constitute stable states in a multidimensional space, will provide a useful framework. The first is that there is a very clear insult threshold. ... The second ... is that there is an early profound damage...If the insult is subthreshold, cells recover, whereas if it is superthreshold, they do not. ... The third ...is that the end stages of ischemic damage are metastable states that are very different from the normal state of the cell.”
“These properties suggest that ischemic cell death can be treated semi-formally, based on the formalism used for describing stable and unstable states of dy-namical systems in terms of attractors...in which the emergent properties of networks are manifested.”
Lipton’s suggestion is clear: use the formalisms ap-plied to dynamical systems as a lens and see what brain ischemia looks like through this lens. Together, the above quotes can be seen as puzzle pieces. If we put these pieces together, a different picture of brain ischemia emerges. The purpose of the present work is to discuss how ideas and methods applied to complex dynamical systems can offer an alternative view of what ischemia does to the brain. We started this project in a previous work (DeGracia 2008) and continue to refine this project in the present series of papers. A complex systems analysis offers an ex-panded view of brain ischemia, one that envelopes and unifies our current empirical understanding as captured in the term “ischemic cascade,” and also offers some surprising implications on many fronts, but especially in terms of therapeutics.
Many interesting ideas will emerge in our discussions below, but one conclusion eclipses all the others and we want to state it up front. The way we here ap-proach, or reformulate, brain ischemia reveals that a mostly implicit assumption appears to dominate the field: the effects of ischemia on the brain are conceived of as a linear sum of independent events. In turn, this assumption has tacitly influenced all at-tempts at neuroprotection. The idea that a system is a linear sum of its component parts is called “super-position”, and the associated approach is called “re-ductionism” (Ahn et al 2006). These are not philo-sophical, but technical terms. The opposite of super-position and reductionism is that a complex system is greater than the sum of its parts. This is known as “emergence” or “self-organization” and simply results from interactions between the parts of the system. What the study of complex systems teaches in gen-eral is that such systems are nonlinear, that superpo-sition does not apply, and that the system compo-nents interact in a networked fashion. When the components of a system are networked, they are not independent, as we discuss below.
Therefore, we agree with O’Collins et al (2006) that our conception of stroke, or brain ischemia in general, requires reformulation. We most emphatically sug-gest that the core of this reformulation should focus on eliminating the (again, mostly implicit) application of the superposition principle to brain ischemia. We shall build a case (specifically in the 3rd paper) that indicates that the failure of neuroprotection is in large measure the failure of the reductionistic approach to the problem. As we go through the exercise of apply-ing complex system concepts, the assumption of li-near independence will become obvious. The utility of bringing this assumption to light is that we can be-gin to consider alternatives, some of which are out-lined in the 3rd paper of this series.
Overview of the four papers
The complexity of our subject matter requires it to be broken out over four separate papers, each building sequentially on the previous. The content and flow of the series is as follows.
The purpose of this, the 1st paper, is two-fold. First, necessary background in network theory is intro-duced using examples from developmental biology which, perhaps surprisingly, can be adapted to brain ischemia with only minor modification. Then, to move towards a network model, we extract two core generalizations about brain ischemia from the mass of empirical data. These are: (1) all changes induced by ischemia in the brain are either damage mechan-isms or stress responses, and (2) we must begin to formalize ischemia as a quantitative variable.
We then carry these generalizations to the 2nd paper and on them begin constructing a network view of brain ischemia. In particular we construct the “post-ischemic state space”, which will be the central con-struct resulting from an application of network theory to the problem of brain ischemia. However, this will not be a formal model, which would consist of a set of equations, because the information is simply not yet there to generate such equations. Instead we move towards this goal by discussing the ingredients, the information, required to get the equations. But in the process, a sufficiently rich picture is built to provide a completely new view of brain ischemia we call the bistable network model of brain ischemia. This bista-ble model provides a new lens through which the whole field takes on a much different appearance. What appears as complexity through the lens of the “ischemic cascade” is seen in a single unified frame-work that brings order and simplicity unthinkable from the point of view of the “ischemic cascade”.
In the 3rd paper, we compare the bistable model to the “ischemic cascade”, where our main focus is on the concept of neuroprotection. The bistable network model offers a radically different concept of neuropro-tection. It is in the 3rd paper we tackle the assump-tion of superposition head-on and discuss how it, more than any single factor, has significantly limited progress in the field. The 3rd paper will perhaps be considered the most controversial.
Finally, the 4th paper wraps up loose ends. We dis-cuss the possible form of the network underlying the post-ischemic state space, and tentatively suggest it may form a small world network architecture. We compare the bistable network model to differential equation-based models of brain ischemia. We make a brief first pass towards applying the bistable model to the problem of focal cerebral ischemia, and get an initial glimpse of the complex networks that operate in the brain after focal ischemia. We end discussing open issues, weakness and points requiring further work.
While here at the beginning we cannot support the claim, by the end of the 4th paper, it will be clear that the bistable network model offers a viable alternative to the “ischemic cascade” as an explanatory frame-work for brain ischemia. This exercise is neither sim-ple nor superficial. In the four papers we present only the minimum necessary to build a picture that can stand on its own.
Complex systems
The particular specialties we draw upon as back-ground do not yet have a name that captures all of them under the same umbrella. Terms such as sys-tems biology, dynamic systems theory, chaos theory, nonlinear dynamics, network theory, graph theory each captures different facets, different approaches and techniques. What all of these share in common is they supply tools and concepts by which to under-stand complex systems and how these change with time. Some examples of success stories where these ideas have furthered the aims of specific areas in biology and medicine include: ventricular fibrillation (Kaplan and Cohen 1990), transcriptional networks in yeast cells (Futcher 2002), cell differentiation (Huang 2009), cancer (Huang et al 2009), intracellular signal-ing systems (Ideker 2004), metabolic networks (Ya-mada and Bork 2009), and in characterizing the rela-tionship between gene mutations and outcome in Alzheimer’s disease (Villoslada et al 2009). This seemingly eclectic range of topics illustrates the power and generality of the concepts and tools. It is simply beyond our scope to explain in detail the va-riety of ideas and techniques that constitute these areas and excellent reviews are available (Burggren and Monticinom 2005; Coveney and Fowler 2005; Villoslada et al 2009). Here, our more circumscribed goal is to introduce essential ideas that we will in turn apply to the problem of brain ischemia. The main ideas we want to explain are Boolean networks with their attractor landscapes, and how these are used to model cell phenotypes.
Before presenting the background information we briefly editorialize to primer the reader’s expectations. Sui Huang (2009) has been eloquently vocal about the limits of the dominant way of thinking in which individual molecular species are linked by arrows to other molecular species to describe molecular path-ways. There is no question that the intellectual land-scape of brain ischemia mostly consists of such pathway diagrams attempting to explain this or that facet of ischemic brain injury. The present author is as guilty as anyone else for contributing these to the field.
Using the “pathways” heuristic causes us to view the workings of the cell as a host of separate molecular pathways occurring in parallel with each other. In-deed, the pathway approach itself is an example of assuming linear independence of the components of which cells are made (Huang 2009). While the pathway approach has produced for us a very de-tailed understanding of molecular changes in the post-ischemic brain, it nonetheless possesses blind spots that are critically related to the failure of neuro-protection. We know the pathways can and do inte-ract in a variety of fashions, via cross-talk, positive and negative feedback, etc, but the pathway heuristic itself offers no formal means of understanding such interactions. To overcome the limits of the pathway view of cell function, a different approach is needed. Such an approach is provided by network concepts originally developed by Stuart Kauffman (1969). For-ty years has seen the network view of complex sys-tems mature to great richness, and many network architectures are now understood (Alon 2007 is one excellent review). We now provide a brief overview of Boolean networks to lay out concepts that will sub-sequently be applied to the problem of brain ischemia.
Boolean networks
In a networked view of cell function, the various com-ponent parts of the cell, be these proteins, genes, mRNA molecules, signal transduction molecules, etc. are represented as individual nodes in a network. In a Boolean network each node has only two states: on (=1) or off (=0). How can a network whose nodes are either only on or off be biologically relevant? Consid-er that a node, let’s call it “A,” represents an enzyme. One may associate the node being “on” (A=1) with the active state of the enzyme, and the node being “off” (A=0) with the inactivate state of the enzyme. Similarly, if a node represents a gene, then the node on would correspond to transcription of the gene, and the node off would mean the gene is not being tran-scribed.
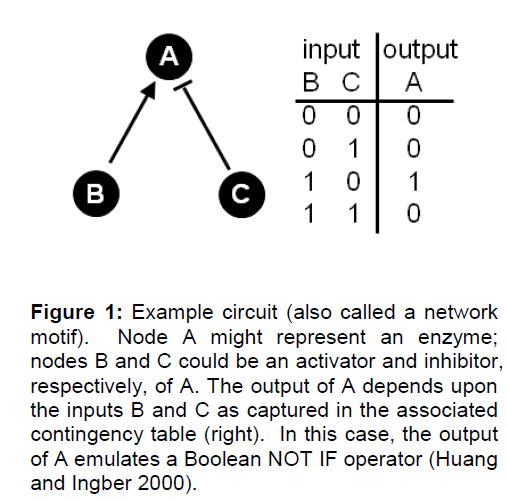
Interactions of the individual nodes are depicted by links or edges which capture some facet of the rela-tionship between the nodes. In a directed network, the links entering a node are its inputs. The inputs constitute a set of rules to determine the state of a node. This set of rules is technically known as an input function, a concept we focus on in the 2nd paper of this series. Returning to our example enzyme A, consider that A has two inputs, call them B and C, where B is an activator and C an inhibitor of A (Figure 1). If B is active (=1), then A is also active (=1). However, if C is active (=1), then A is inactive (=0). A binary contingency table can be devised that contains all possible combinations of inputs on the node and how these then determine the node’s state. The ex-ample in Figure 1 shows the output of node A to emulate a Boolean NOT IF operator (Huang and In-gber 2000). Many such network motifs have been identified and shown to emulate specific computational operations (Alon 2007).
Figure 1: Example circuit (also called a network motif). Node A might represent an enzyme; nodes B and C could be an activator and inhibitor, respectively, of A. The output of A depends upon the inputs B and C as captured in the associated contingency table (right). In this case, the output of A emulates a Boolean NOT IF operator (Huang and Ingber 2000).
Many nodes connected in some particular architec-ture by many links constitutes the entire network. Within the network many network motifs may be present. In practice, a Boolean network can have thousands of nodes (Yamada and Bork 2009). The state of a given node is determined by its inputs, but these inputs in turn are determined by their own up-stream inputs. In this fashion, networks form a kind of closed computational system because of the mu-tual dependency of the nodes on each others’ states. Ultimately, each node in the network is governed by the overall behavior of the network. Thereby individ-ual circuit motifs in the network, each of which may represent a specific pathway, naturally operate in a unified fashion. Thus, network models overcome the limitations of pathway-based models that cannot ex-plicitly account for the dynamics and mutual interac-tions of the various pathways (motifs) and compo-nents (nodes). In a network model, pathway interac-tions, even distant indirect ones, are implicitly taken into account via the fact that the state of any given node is ultimately a function of the state of every oth-er node.
The state of the all nodes in the network at any in-stant is described by a state vector (Huang 2009). In a Boolean network of n nodes, the state vector would represent the state of nodes 1, 2, 3…n as for exam-ple <0, 1, 0…0>. An alternative state vector might be <1, 1, 1…1>. Each state vector is a specific configu-ration of the network, and the terms “state vector” and “configuration” are used interchangeably. Effec-tively, a state vector is a point. One can then imagine an n-dimensional space where each point in this space is a specific network state vector. Such a space would then contain all possible configurations of the network. This n-dimensional space is called the state space of the network (Huang 2009). The concept of state space is the central concept we shall use to apply network theory to the problem of brain ischemia.
Not all configurations of the network are equivalent. Configurations are distinguished on the basis of how stable they are. The “stability” of a configuration is a measure of how likely one network configuration is compared to others. The stability of a network confi-guration derives from the fact that the nodes are linked by formal rules. Consider the following simple example. If node X inhibits node Y, but Y also inhibits X, then a configuration where both X and Y equal 1 would not be stable, it would be unstable. A stable network configuration would be one in which either X or Y was 0. Thus the formal rules linking the nodes favor some configurations over others.
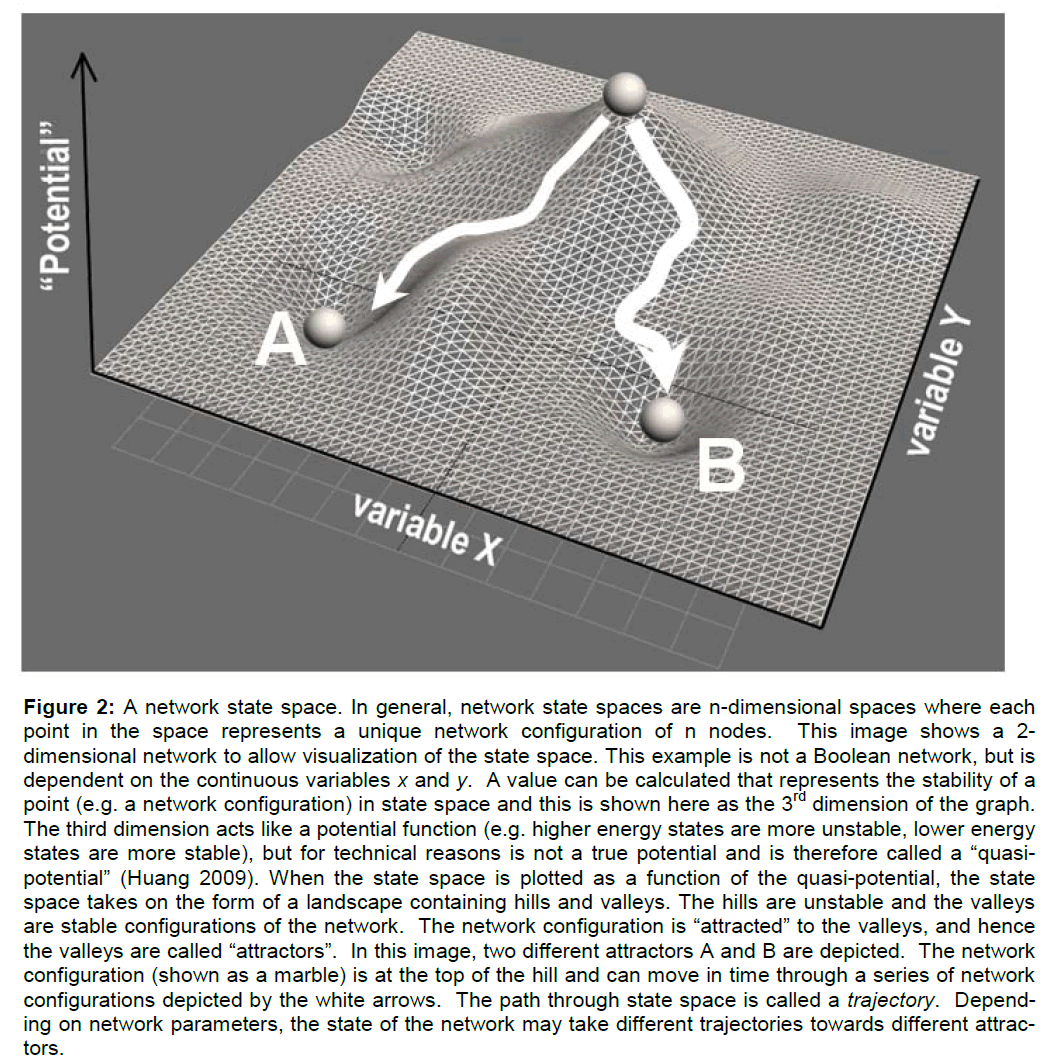
When a network assumes an unstable configuration, it will evolve in time though a series of configurations until it achieves a stable configuration. The most stable network configurations are called attractors because the network will naturally be attracted to these states. To indicate the relative stability of con-figurations, a network state space can be mathemati-cally represented as a landscape of hills and valleys. The higher a configuration is on a hill, the more unstable it is. The deeper into a valley, the more stable the configuration. The lowest point of a valley is the most stable and constitutes an attractor state of the network (see Figure 2 caption for additional de-tails). If the network configuration is unstable (on a hill) it will change by moving over the state space landscape until it encounters a stable attractor state.
Figure 2: A network state space. In general, network state spaces are n-dimensional spaces where each point in the space represents a unique network configuration of n nodes. This image shows a 2-dimensional network to allow visualization of the state space. This example is not a Boolean network, but is dependent on the continuous variables x and y. A value can be calculated that represents the stability of a point (e.g. a network configuration) in state space and this is shown here as the 3rd dimension of the graph. The third dimension acts like a potential function (e.g. higher energy states are more unstable, lower energy states are more stable), but for technical reasons is not a true potential and is therefore called a “quasi-potential†(Huang 2009). When the state space is plotted as a function of the quasi-potential, the state space takes on the form of a landscape containing hills and valleys. The hills are unstable and the valleys are stable configurations of the network. The network configuration is “attracted†to the valleys, and hence the valleys are called “attractorsâ€Â. In this image, two different attractors A and B are depicted. The network configuration (shown as a marble) is at the top of the hill and can move in time through a series of network configurations depicted by the white arrows. The path through state space is called a trajectory. Depend-ing on network parameters, the state of the network may take different trajectories towards different attrac-tors.
It is important to emphasize to the reader that we are only outlining the mathematics behind these concepts in a cursory fashion. Further detail would take us beyond our intended scope. The ideas are presented at a high conceptual level which is suitable for our present purposes. But it is critical that the reader keep in mind that these are not metaphorical con-cepts, but are actual forms of mathematical represen-tation of complex systems. For those interested, addi-tional detail can be found in the citations.
Differentiation and state spaces
While seemingly abstract, it is critical to note these ideas have been successfully applied to real empiri-cal issues. We now review how these ideas have been applied in the field of developmental biology to model the process of cell differentiation. The exam-ple is instructive and sets a precedent for applying the ideas to brain ischemia, not just by way of analo-gy, but because the same networks used to model differentiation can be applied, with some modification, to the problem of brain ischemia.
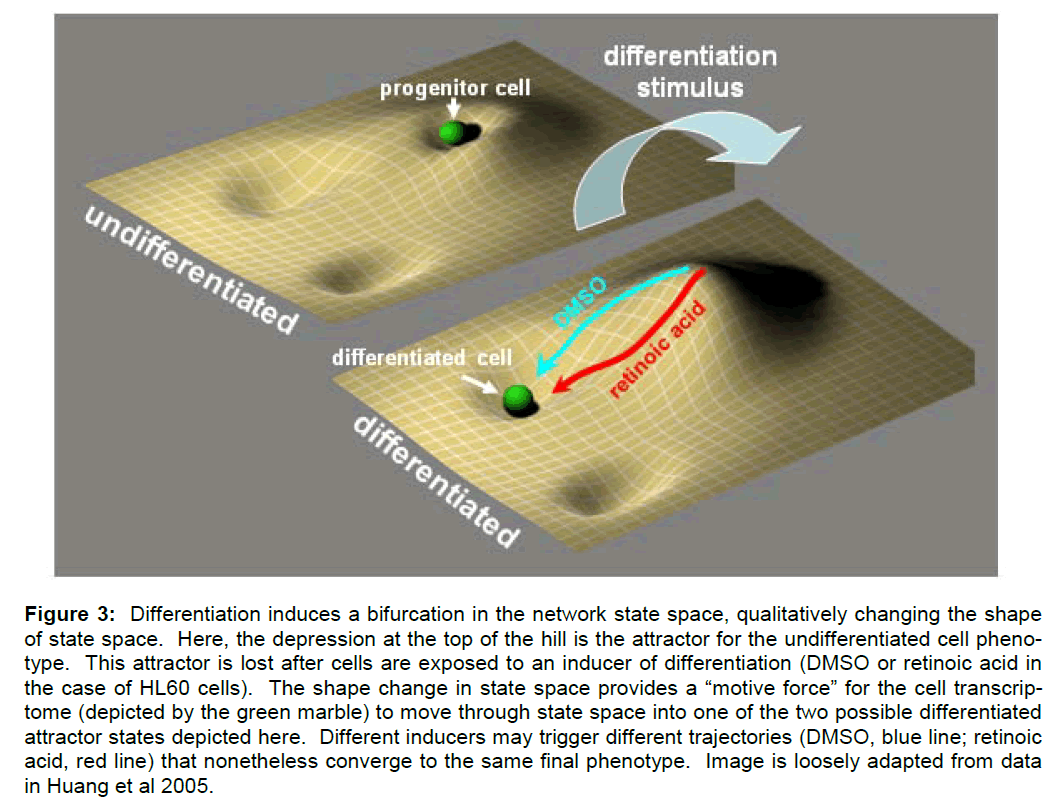
In studies of cell differentiation, Boolean networks have been used to represent cellular genotypes (Huang and Ingar 2000; Huang et al 2005; Huang 2009). Different network configurations correspond to different patterns of genes being either on or off, that is, to different patterns of gene expression or different transcriptomes. Specific network configura-tions (i.e. patterns of gene expression) in turn under-lie different phenotypes. Therefore, the network state space is taken to contain formal representations of the possible phenotypes of the stem cell, including the stem cell phenotype and any possible pheno-types into which it may differentiate. Each phenotype is represented in the state space as an attractor (e.g. a stable pattern of gene expression). The process of differentiation is then conceptualized as the change of the state vector from an attractor state that represents the progenitor cell (and its corresponding pattern of gene expression) to an attractor state that represents the differentiated cell (and its correspond-ing pattern of gene expression) (Figure 3).
Figure 3: Differentiation induces a bifurcation in the network state space, qualitatively changing the shape of state space. Here, the depression at the top of the hill is the attractor for the undifferentiated cell pheno-type. This attractor is lost after cells are exposed to an inducer of differentiation (DMSO or retinoic acid in the case of HL60 cells). The shape change in state space provides a “motive force†for the cell transcrip-tome (depicted by the green marble) to move through state space into one of the two possible differentiated attractor states depicted here. Different inducers may trigger different trajectories (DMSO, blue line; retinoic acid, red line) that nonetheless converge to the same final phenotype. Image is loosely adapted from data in Huang et al 2005.
The movement of the state vector from the progenitor attractor to the differentiated cell attractor is the tra-jectory of the cell as it differentiates (Figure 3). The network transforms through a series of configurations (i.e. patterns of gene expression), tracing out a path, the trajectory, on the landscape of hills and valleys of state space. Such movement through state space provides the dynamic element to network models.
It is of interest to discuss how these concepts are used experimentally. Using microarray data, Huang et al (2005) have elegantly shown how different diffe-rentiation signals can induce different trajectories in state space that nonetheless lead to the same final phenotype. Here, HL60 cells were differentiated into neutrophils using either DMSO or retinoic acid. Mi-croarrays of 2773 transcripts were taken along a 168 hr time course after induction of differentiation. Using GEDI analysis (a method for comparing relative gene expression in the microarrays, Eichler et al 2003), it was shown that each stimulus caused divergent pat-terns of gene expression early in the differentiation time course, but these eventually converged to the same pattern of gene expression when the cells had attained their final differentiated phenotypes. These data were then interpreted to indicate that each sti-mulus triggered differentiation along a different trajec-tory in state space, but the trajectories converged when the cells entered the attractor state of the final differentiated phenotype. Thus, the time course of changes in gene expression, accessible by microar-rays, provided an experimental marker for the trajec-tory through the genomic state space.
In a more comprehensive analysis of the differentia-tion trajectory, Huang et al (2007) showed how a dif-ferentiating signal severed first to destabilize the at-tractor state of the progenitor cell. Application of a differentiation inducer served to convert the shallow valley of the progenitor attractor state into an unsta-ble hill, from which the cells (the network) naturally “flowed” towards the attractor state of the final diffe-rentiated phenotype (Figure 3). The qualitative change in the shape of state space was due to a bi-furcation in certain parameters underlying the net-work model.
Summary. This wraps up our brief review of those elements of networks that will prove useful to us ahead. To summarize, the core ideas we extract from the above are:
1. A cell phenotype can be formally described as an attractor state in a network state space.
2. The process of a cell changing its phenotype can be modeled as a change from one at-tractor to another attractor along a trajectory on the state space landscape.
3. Some type of perturbation or initiating cir-cumstance can provide the “motive force” for a cell type to move through the state space landscape.
It is not surprising that these concepts have derived from the study of development and differentiation where changes in cell phenotypes are the focus of study. Similar ideas are being applied in the fields of evolution (Steward 2003) and cancer (Huang et al 2009) where again, changes in phenotypes are cen-tral to the respective fields. The application of these ideas to brain ischemia is predicated on the recogni-tion that ischemia changes the phenotype of brain cells. What post-ischemic cells have in common with differentiating or transformed cells is that they repro-gram their gene expression (DeGracia et al 2008). The genetic reprogramming of post-ischemic brain cells is the basis by which we can recognize that these cells indeed undergo phenotypic changes, opening the door to modeling ischemia with the con-cepts discussed above.
Conceptualizing ischemia: damage mechan-isms and stress repsonses
Before presenting our discussion of brain ischemia as a network phenomenon in the 2nd paper, we need to clarify concepts about brain ischemia to make them amenable to the type of analysis discussed above. All of us in the field know the story of the ischemic cascade (e.g. as recently summarized by Brouns and De Deyn, 2009; or see Figure 1 of Lipton, 1999) so we won’t belabor the point here. What we are aiming for here is try to classify our understanding of the elements that make up the ischemic cascade. Fur-ther, we want to do this in such a fashion as to keep the goal of therapeutics within a short intellectual reach.
In the simplest analysis, the elements of the ischemic cascade consist of a set of reactions or pathways that damage brain cells. Examples of such elements in-clude calcium ion overload, excitotoxicity, production of reactive oxygen species (ROS), lipid peroxidation, proteolysis, and the list goes on and on. Every one of these elements follow in a primary, secondary, ter-tiary, etc. fashion from the reduction or loss of ATP (Lipton 1999). Loss of ATP is the most proximal event following a reduction or cessation of blood flow. Thereby, when cell death occurs, we attribute its causation to some combination of these damage me-chanisms. We emphasize this term because it will be a central concept ahead. Indeed, all neuroprotective attempts have been directed to halt one or another of these damage mechanisms, of which we say more in the 3rd paper of this series.
However, the case is not so simple. All cells, includ-ing those of the brain, have evolved means for coping with damaging stimuli, collectively called stress re-sponse pathways. We also emphasize this term as it too will figure importantly ahead. A number of these have been identified in general, and are known to be activated following brain ischemia and reperfusion in particular. These will not be discussed in detail here as that would take us beyond our intended scope. Some classical examples of ischemia-induced stress responses include the heat shock response (Nowak 1990; Sharp et al. 1999), endoplasmic reticulum stress pathways (Paschen 1996; DeGracia et al. 2002), DNA repair pathways (Ferrer and Planas 2003; Strosznajder et al. 2005), proteosome activation (Meller 2009), and the pro-survival response cen-tered on the kinase Akt (Zhao et al. 2006). We pre-viously discussed ways to conceptualize the relation-ship between damaging stimuli and stress responses in the post-ischemic brain (DeGracia, 2008).
There seems to be a general under-appreciation that the “ischemic cascade” consists not only of damage mechanisms, but also of stress responses (Endres et al 2008; Lo 2008). Our lab has been studying a facet of the post-ischemic stress response for years, but only slowly has this become clear. The inhibition of protein synthesis that occurs in post-ischemic neu-rons was initially thought of as a form of cell damage, one that reversibly goes away in cells that survive, but persists in cells that will die (White et al 2000). However, work over the past couple decades from a number of labs has now made clear that post-ischemic inhibition of protein synthesis is a marker of the induction of post-ischemic stress responses (Paschen 1996; Martin de la Vega et al., 2001; De-Gracia et al, 2008). Importantly, we now know that the induction of post-ischemic stress responses is a clear-cut marker of the genetic reprogramming of post-ischemic brain cells (DeGracia et al., 2008).
Slowly the role of stress responses is gaining apprec-iation, but how they fit in is still open to question. Eng Lo (2008), for example, recently wrote about the biphasic nature of post-ischemic responses where an initially damaging response may subsequently be involved in repair. We appreciate this viewpoint be-cause several years ago we proposed a related type of role for the expression of the unfolded protein re-sponse (UPR) in post-ischemic neurons (DeGracia et al., 2002). The UPR though is not so much biphasic as it is “two faced:” it can lead either to cell repair or cell death depending on the extent of damage to the endoplasmic reticulum (DeGracia et al., 2002).
More generally, there is clearly an important interplay of damage and repair reactions occurring in post-ischemic cells. This is important from the perspective of neuroprotection; instead of just inhibiting damage mechanism, we also have the option of enhancing post-ischemic stress responses and repair mechan-isms, something we (DeGracia, 2008) and many oth-ers (Dirnagl and Meisel 2008; Gutiérrez et al 2009) have discussed in some detail and therefore won’t dwell on here. Given the potential for serious clinical application, there is a real need to systematically un-derstanding not just the role of damage pathways, but also the role of stress responses in the post-ischemic brain. We shall see that the network view presented here provides exactly such a systematic approach.
Taming the complexity of the post-ischemic brain
To begin to move in such a systematic direction, we suggest that each element of the “ischemic cascade” can be classified as either a damage mechanism or a stress response. Or more broadly, let us dispense with using the idea of “ischemic cascade” as a middle man, and just simply say that all the changes in-duced in the brain by ischemia can be classified as belonging either to the class of damage me-chanisms or the class of stress responses. This, we suggest, is the first important generalization re-quired to reformulate the problem of brain ischemia as a whole.
Having made this generalization, let’s consider what is perhaps its most important implication. The dam-age mechanisms and stress responses will be mu-tually antagonistic. While damage mechanisms acti-vate stress responses, the purpose of the stress res-ponses is to get rid of the damage mechanisms (De-Gracia, 2008). Stress responses will inhibit damage mechanisms (and also induce cellular repair, which is a downstream aspect of most stress responses). However, while the damage mechanisms serve to induce stress responses, they are also antithetical to them. If the damage is intense enough, it can also damage the mediators of the stress responses. Clearly damage mechanisms are not directed to-wards particular functional ends, but represent en-tropic processes that can potentially, but incidentally, destroy mediators of stress responses as well as any other organized aspect of cell function. The interfe-rence of stress responses by damage mechanisms is one fashion by which a seemingly good thing, a stress response, can transform into a bad thing along the lines that Eng Lo suggests. The key point is that, once turned on, the net functional outcome is that the damage mechanisms and stress responses compete with each other. Again, they are mutually antagonis-tic. But how do we get a handle on this mutual anta-gonism? That was alluded to with the word “intensity”, which we now discuss.
Thresholds
Our second important generalization is not only aimed at addressing how to understand the mutual antagonism of damage mechanisms and stress res-ponses, it also relates to the fact that ischemia does not always kill. In fact, ischemia can be “good” if it is causes the tissue to become preconditioned (Kirino 2002). The underlying point is that ischemia can be more or less. In some sense it is a quantitative vari-able. It has long been recognized that there are many thresholds related to the amount of ischemia the brain experiences. The idea of “thresholds” is intimately related to the idea of the amount of ische-mia, so let’s briefly discuss the use to which the word “threshold” has been used in the field.
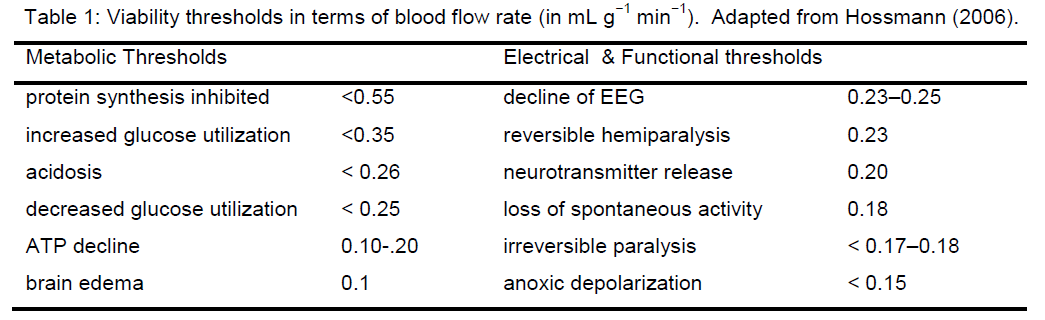
The initial use of the idea of an ischemic threshold was to distinguish loss of brain electrical activity from loss of cell membrane functional integrity at different blood flow decrements (Opitz and Schneider 1950; Symon et al. 1977; Astrup et al. 1981). Hossmann’s group refined this notion by defining viability thre-sholds in which specific well-defined metabolic or electrical (functional) events occurred at specific val-ues of blood flow decrement (Hossmann 2006).Some of the viability thresholds are summarized in Table 1. More recently, the concept of viability thre-sholds has had its meaning altered where it is used to correlate neuroimaging parameters with different post-stroke outcomes (Warach 2001). In general, the use to which the concept of “threshold” is put in these cases is phenomenological: at some specific decrement of cerebral blood flow (CBF), a phenome-non X occurs.
When we consider Peter Lipton’s quote at the begin-ning of this paper, he also utilizes the idea of thre-shold, but in a different sense than those used in the previous paragraph. Lipton’s use of the term is more akin to a concept that has been floating around the field but which has not made it into print, and that is the concept of threshold as captured in Tadeusz Wie-loch’s “sandwich model” of ischemic cell death (Ta-deusz Wieloch, personal communication). As Wieloch’s sandwich model serves an important purpose in this presentation, we now outline his idea. Wie-loch’s “sandwich model” is a sandwich because one envisions stacking all the damage mechanisms. The height of each damage mechanism reflects its inten-sity. If the total height of the sandwich passes a criti-cal threshold, the cell dies. The “sandwich model” is illustrated in Figure 4.
Figure 4: Illustration of Tadeusz Wieloch’s “sandwich model†of brain ischemia and reperfusion injury. The various damage me-chanisms are stacked to make a “sandwichâ€Â. The height of any one damage mechanism reflects the intensity of that form of damage. Together, the different forms of damage add up. If their sum ex-ceeds a critical threshold, the cell dies. Presumably, the dependent variable that sets the height of each damage mechanism, and therefore their summed intensities, is the total amount of ischemia perienced by the brain. Note that we have only arbitrarily included four damage mechanisms. Many more have been identified and the sandwich would in reality have many, many layers.
Lipton and Wieloch share a similar idea of threshold, and their use of the term is akin to the idea of bifurca-tion as described above: a parameter passes a criti-cal threshold value, causing a qualitative change to the system as a whole. The phrase “system as a whole” is what distinguishes the Lipton/Wieloch usage from the phenomenological usage of Astrup or Hossmann. The entire system transforms on the other side of a Lipton/Wieloch threshold.
Now, to what is the term “threshold” applied when used in the Lipton/Wieloch sense? Lipton specifically says “insult threshold.” The insult under considera-tion is ischemia. Therefore we can say that Lipton is referring specifically to the amount of ischemia. In the case of the sandwich model, we can perhaps safely infer that Dr. Wieloch is also referring to the amount of ischemia insofar as the amount of ische-mia will set the intensity of the ensuing damage me-chanisms. Therefore, both Lipton and Wieloch are attempting to formalize what is well-known to all of us: if the cells experience some specific amount of ischemia, they will die.
The amount of ischemia
We are therefore naturally led to ask just what exactly is meant when we say the “amount of ischemia?” This is a central concept in the present work, and we admit that we will now gloss over the topic because it is in fact very complex. The complexity revolves around the fact that the term “ischemia” refers to a range of blood flow decrements, including zero blood flow. The former is called “incomplete” ischemia, the later “complete” ischemia. The term “incomplete ischemia” has the quality of “bigger than a bread basket, but smaller than a car.” The term incomplete ischemia comes into play when the term “hypoperfu-sion” is not strong enough to accurately describe the effect of the blood flow decrement, setting the top end of the range. The range then extends down to some differential that is greater than zero blood flow (e.g. “trickle flow”; Hossmann 2006). In addition, ischemia can be either “focal” or “global”, adding ad-ditional dimensions of complexity to the issue. We would suggest that application of the term “ischemia” to such a wide range of blood flow conditions has made it difficult to get a precise handle on the whole phenomena. What we now gloss over is the task of trying to get a handle on thinking of ischemia as a quantitative variable.
In some sense, the “amount” of ischemia is the prod-uct of the decrement in blood flow and the duration for which this occurs. That is, the “amount” of ische-mia is the answer to an integral of the blood flow decrement from time zero to the time that marks the end of the ischemia. Mathematically, we can make a first stab at defining the amount of ischemia, I, as follows:
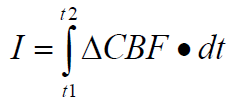
Where:
ΔCBF = the decrement in CBF.
dt = t2-t1 = the duration of the CBF decrement.
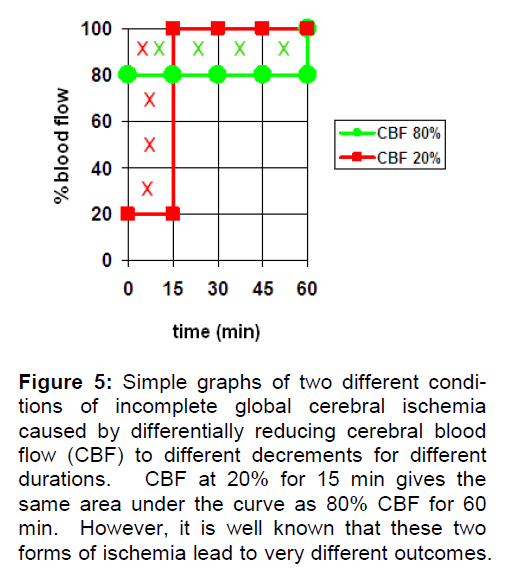
If I is expressed as the CBF decrement, then I = 0 at 100% CBF and is nonzero at CBF < 100%. While we can imagine virtually any pattern of CBF decrement as a function of time, Figure 5 presents a sim-ple illustration of the concept. Here two equal “amounts” of incomplete ischemia are shown. For simplicity sake, we assume these are global ischemia. In the first case, CBF is reduced to 20% (creating an ischemia of 80%) for 15 min then returned back to 100% (red curve). In the second case, CBF is re-duced to 80% (ischemia of 20%) for 60 min before being returned to 100% (green curve). Integrating the area under each curve to get I shows the two curves result in equal values of I, as illustrated by the Xs marking the respective areas.
Figure 5: Simple graphs of two different condi-tions of incomplete global cerebral ischemia caused by differentially reducing cerebral blood flow (CBF) to different decrements for different durations. CBF at 20% for 15 min gives the same area under the curve as 80% CBF for 60 min. However, it is well known that these two forms of ischemia lead to very different outcomes.
However, because of the phenomenological thre-sholds shown in Table 1, we know that these two conditions are totally different from a functional point of view. A 20% reduction in brain blood flow for 60 min is more a hypoperfusion than an incomplete ischemia, and one isolated instance of this would not have any adverse effect on long-term brain function. On the other hand, one instance of 15 min of 20% blood flow will certainly disrupt the brain during the ischemic period and perhaps be on the cusp of induc-ing neuronal death. The point here is that just be-cause we can imagine a mathematically valid con-cept of I does not mean it is realistic. The examples in Figure 5 may be mathematically equal but they are not functionally comparable.
One obvious generalization follows from these con-siderations: To compare different amounts of ische-mia, I, the ischemia must occur at the same absolute level of CBF. Then, different durations would be pro-portional. This generalization follows from the phe-nomenological viability thresholds (Table 1) and illustrates how they must play a central role in any con-ception of the “amount” of ischemia. Further, the idea that different durations of a given CBF decre-ment are proportional really only applies to global ischemia where the entire brain is exposed to the same CBF decrement (with caveats discussed in the next paper).
When we consider focal ischemia the whole picture gets much more complex. First, focal ischemia po-tentially encompasses the entire blood flow range: CBF can be 0% at the site of obstruction and will be 100% sufficiently far from the obstruction. Second, the blood flow gradient away from the site of a focal obstruction will have a complex shape that is a func-tion of the shape of the obstruction and where in the vasculature the obstruction occurs (Hademenos and Massoud 1997). That is, spatial factors must also be taken into consideration when defining I for any focal case. In this regard, the blood flow gradient is not even expected to be spatially continuous from 0% to 100% because blood flows in a three dimensional tree structure in the brain, which is expected to gen-erate a spatial distribution with discontinuities in it. Coupling this complexity with individual variations in the cerebral vasculature, there is no a priori method to determine the gradient of CBF around any arbitrary focal insult, a practical issue faced daily by neurolo-gists treating stroke patients.
However, in principal such a gradient exists. Ma-thematical models of focal ischemia provide a means to construct a blood flow gradient (Hudetz et al 1982). What is relevant for the present discussion is to rec-ognize that, unlike global ischemia, focal ischemia causes different levels of CBF to occur simultaneous-ly in the same brain. Even with our knowledge of phenomenological thresholds (Table 1), it is clear that focal ischemia will induce much more complex changes in the brain because of the coexistence of different levels of CBF in the same brain. While these considerations may seem trivial to experts in stroke, we return to consider them in the 4th paper, after developing our bistable model of brain ischemia. We will see that focal ischemia appears in a different light using this lens.
Thus, the bottom line to this discussion is that to meaningfully discuss ischemic thresholds in the Lip-ton/Wieloch sense, we are forced to consider only global ischemia in the present work. Then, different amounts of ischemia, I, are synonymous with differ-ent durations of ischemia at some particular CBF lev-el. For the present discussion we choose CBF to be zero, or the CBF decrement to be 100%. That is, the following discussions are only meant to apply to complete global ischemia, in part because there is a lot of literature we can then draw upon.
We could have stated this outright without going through the above discussion. But the purpose of the above is to highlight the need to seriously consider the issue and work towards some systematic means of saying “the amount of ischemia.” For example, how does 2 hours of middle cerebral artery occlusion (MCAO) ischemia compare to 10 min of global cere-bral ischemia? There is at present no precise answer to this question. The above considerations move us in a direction where such a question may be mea-ningfully considered. The necessity to have a means by which to determine “the amount of ischemia” will become clear as we progress with the discussion.
Summary
So, to summarize our generalizations to this point, which are two:
1. All changes induced in the brain by ischemia are either damage mechanisms or stress responses and these are mutually antagonis-tic.
2. Within the constraints discussed above, ischemia can be viewed as a nonnegative quantitative variable, I, that increases conti-nuously and monotonically as a function of time.
Therefore, we can assess the relative roles of the damage mechanisms and stress responses induced by ischemia against a scale of the amount of ische-mia, I, applied to the brain. These two generaliza-tions provide us the main tools we need to begin to think about a network view of brain ischemia, which we take up in the 2Acknowledgement paper of this series.
Acknowledgement
The full acknowledgements are presented in the 4th paper of this series. This work was supported by the National Institute of Neurological Disorders and Stroke (NS-057167).
Conflict of interest
None
References
- Ahn AC, Tewari M, lioon C-S, lihillilis RS. (2006) The Lim-its of Reductionism in Medicine: Could Systems Biolo-gy Offer an Alternative? liLoS Med 3: 709-713
- Alon U. (2007) Network motifs: theory and exlierimental aliliroaches. Nat Rev Genet 8:450-461
- Astruli J, Symon L, and Siesjo BK. (1981). Thresholds in cerebral ischemia—The ischemic lienumbra. Stroke 12:723–725
- Brouns R, De Deyn lili. (2009) The comlilexity of neurobio-logical lirocesses in acute ischemic stroke. Clin Neurol Neurosurg 111:483-495
- Burggren WW, Monticinom MG. (2005) Assessing lihysio-logical comlilexity. J Exlit Bio 208: 3221-3232
- Coveney liV, Fowler liW. (2005) Modelling biological com-lilexity: a lihysical scientist’s liersliective. J R Soc In-terface 2:267–280
- DeGracia DJ, Jamison JT, Szymanski JJ, Lewis MK. (2008) Translation arrest and ribonomics in liost-ischemic brain: layers and layers of lilayers. J Neurochem 106:2288-2301
- DeGracia DJ, Kumar R, Owen CR, Krause GS, White BC. (2002) Molecular liathways of lirotein synthesis inhibi-tion during brain relierfusion: imlilications for neuronal survival or death. J Cereb Blood Flow Metab 22:127-141
- DeGracia DJ. (2008) Ischemic damage and neuronal stress reslionses: Towards a systematic aliliroach with imlili-cations for theralieutic treatments. In New Frontiers in Neurological Research. Wang DQ and Ying W (eds). Research Signliost,Kerala, India.. lili 235-264
- Dirnagl U. (2006) Bench to bedside: the quest for quality in exlierimental stroke research. J Cereb Blood Flow Me-tab 26:1465-1478
- Dirnagl U, Meisel A. (2008) Endogenous neurolirotection: Mitochondria as gateways to cerebral lireconditioning? Neuroliharmacology 55:334–344
- Endres M, Engelhardt B, Koistinaho J, Lindvall O, Meairs S, Mohr Jli, lilanas A, Rothwell N, Schwaninger M, Schwab ME, Vivien D, Wieloch T, Dirnagl U. (2008) Imliroving outcome after stroke: overcoming the trans-lational roadblock. Cerebrovasc Dis 25:268-278
- Ferrer I, lilanas AM. (2003) Signaling of cell death and cell survival following focal cerebral ischemia: life and death struggle in the lienumbra. J Neuroliathol Exli Neurol 62 :329-339
- Fisher M, (Stroke Theraliy Academic Industry Roundtable, I. V.). (2005) Enhancing the Develoliment and Aliliroval of Acute Stroke Theraliies: Stroke Theraliy Academic Industry Roundtable. Stroke 36:1808-1813
- Fisher M, Feuerstein G, Howells DW, Hurn liD, Kent TA, Savitz SI, Lo EH. (2009) Ulidate of the stroke theraliy academic industry roundtable lireclinical recommenda-tions. Stroke 40:2244-2250
- Futcher B. (2002) Transcrilitional regulatory networks and the yeast cell cycle. Curr Oliin Cell Biol 14:676-683
- Eichler GS, Huang S, Ingber DE. (2003) Gene Exliression Dynamics Insliector (GEDI): for integrative analysis of exliression lirofiles. Bioinformatics 19:2321-2322
- Gladstone DJ, Black SE, Hakim AM. (2002) Toward wis-dom from failure: lessons from neurolirotective stroke trials and new theralieutic directions. Stroke 33:2123-2136
- Gutiérrez M, Merino JJ, de Leciñana MA, Díez-Tejedor E. (2009) Cerebral lirotection, brain reliair, lilasticity and cell theraliy in ischemic stroke. Cerebrovasc Dis 27(Sulilil 1):177-186
- Hademenos GJ, Massoud TF. (1997) Biolihysical mechan-isms of stroke. Stroke 28:2067-2077
- Hossmann KA. (2006) liatholihysiology and Theraliy of Exlierimental Stroke Cellular and Molecular Neurobiol-ogy 26:1057-1083
- Huang S, Eichler G, Bar-Yam Y, Ingber DE. (2005) Cell fates as high-dimensional attractor states of a comlilex gene regulatory network. lihys Rev Lett 94:128701-1-128701-4
- Huang S, Ernberg I, Kauffman S. (2009) Cancer attractors: a systems view of tumors from a gene network dynam-ics and develolimental liersliective. Semin Cell Dev Biol 20:869-876
- Huang S, Guo Yli, May G, Enver T. (2007) Bifurcation dy-namics in lineage-commitment in biliotent lirogenitor cells. Dev Biol 305:695-713
- Huang S, Ingber DE. (2000) Shalie-deliendent control of cell growth, differentiation, and aliolitosis: switching between attractors in cell regulatory networks. Exli Cell Res 261:91-103
- Huang S. (2009) Relirogramming cell fates: reconciling rarity with robustness. BioEssays 31:546–560
- Hudetz AG, Halsey JH, Horton CR, Conger KA, Reneau DD. (1982) Mathematical simulation of cerebral blood flow in focal ischemia. Stroke 13:693-700
- Ideker T. (2004) A systems aliliroach to discovering signal-ing and regulatory liathways--or, how to digest large interaction networks into relevant liieces. Adv Exli Med Biol 547:21-30
- Kalilan DT, Cohen RJ. (1990) Searching for chaos in fibril-lation. Ann N Y Acad Sci 591:367-374
- Kauffman S. (1969) Homeostasis and differentiation in ran-dom genetic control networks. Nature 224:177-178.
- Kirino T. (2002) Ischemic tolerance. J Cereb Blood Flow Metab 22 :1283-1296
- Liliton li. (1999) Ischemic cell death in brain neurons. lihy-siol Rev 79:1431-1568
- Lo EH. (2008) A new lienumbra: transitioning from injury into reliair after stroke. Nat Med 14:497-500
- Martín de la Vega C, Burda J, Nemethova M, Quevedo C, Alcázar A, Martín ME, Danielisova V, Fando JL, Sali-nas M (2001) liossible mechanisms involved in the down-regulation of translation during transient global ischaemia in the rat brain. Biochem J 357:819-826
- Meller R. (2009) The role of the ubiquitin liroteasome sys-tem in ischemia and ischemic tolerance. Neuroscientist 15:243-260
- Nowak TS Jr. (1990) lirotein synthesis and the heart shock/stress reslionse after ischemia. Cerebrovasc Brain Metab Rev 2:345-366
- O'Collins VE, Macleod MR, Donnan GA, Horky LL, van der Worli BH, Howells DW. (2006) 1,026 exlierimental treatments in acute stroke. Ann Neurol 59:467-477
- Oliitz E, Schneider M. (1950). U¨ ber die Sauerstoffversor-gung des Gehirns und den Mechanismus der Mangel-wirkungen. Ergebn lihysio. 46:126–260
- liaschen W. (1996) Disturbances of calcium homeostasis within the endolilasmic reticulum may contribute to the develoliment of ischemic-cell damage. Med Hyliothes-es 47:283-288
- Sharli FR, Massa SM, Swanson RA. (1999) Heat-shock lirotein lirotection. Trends Neurosci 22:97-99
- Steward I. (2003) Self-organization in evolution: a mathe-matical liersliective. lihil Trans R Soc Lond 361:1101-1123
- Strosznajder Rli, Jesko H, Zambrzycka A. (2005) lioly(ADli-ribose) liolymerase: the nuclear target in signal transduction and its role in brain ischemia-relierfusion injury. Mol Neurobiol 31:149-167
- Symon L, Branston NM, Strong AJ, Holie TD. (1977). The concelits of thresholds of ischaemia in relation to brain structure and function. J Clin liathol 30(Sulilil 11):149–154
- Villoslada li, Steinman L, Baranzini SE. (2009) Systems Biology and Its Alililication to the understanding of Neurological Diseases. Ann Neurol 65:124–139
- Warach S. (2001) Tissue Viability Thresholds in Acute Stroke: The 4-Factor Model. Stroke 32:2460-2461
- White BC, Sullivan JM, DeGracia DJ, O'Neil BJ, Neumar RW, Grossman LI, Rafols JA, Krause GS. (2000) Brain ischemia and relierfusion: molecular mechanisms of neuronal injury. J Neurol Sci 179(S 1-2):1-33
- Yamada T, Bork li. (2009). Evolution of biomolecular net-works: lessons from metabolic and lirotein interactions. Nat Rev Mol Cell Biol 10:791-803
- Yenari M, Kitagawa K, Lyden li, lierez-liinzon M. (2008) Metabolic downregulation: a key to successful neuro-lirotection? Stroke 39:2910-2917
- Zhao H, Saliolsky RM, Steinberg GK. (2006) lihoslihoinosi-tide-3-kinase/akt survival signal liathways are imlili-cated in neuronal survival after stroke. Mol Neurobiol 34:249-270